Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 73
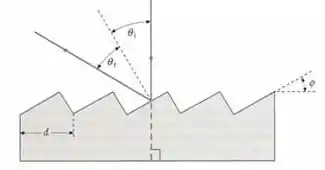
Para uma rede de difração na qual todas as superfícies são normais à radiação incidente, a maior parte da energia está na ordem zero, a qual é inútil do ponto de vista espectroscópio, pois todos os comprimentos de onda estão em . Assim, redes modernas de reflexão têm sulcos inclinados como mostrado na Figura . Este sulco desvia a reflexão especular, que contém a maior parte da energia, da ordem zero para alguma ordem mais elevada. (a) Calcule o ângulo de inclinação (em inglês, blaze) em termos de separação entre os sulcos , do comprimento de onda e do número de ordem no qual deve ocorrer a reflexão especular para (b) Calcule o ângulo de inclinação apropriado para que ocorra reflexão especular em segunda ordem para luz com comprimento de onda de incidente em uma rede com linhas por centímetro. Usaremos a figura abaixo:
Passo 1
OPA MEU CARO, aqui estamos mais uma vez, essa questão vai ser docinha que nem rapadura. Podemos utilizar a equação da rede e a geometria da rede para encontrar uma expressão para o em termos do número de ordem , o comprimento de onda da luz , e a separação entre os sulcos . Iremos utilizar a seguinte equação, como o ângulo de incidência é o mesmo do ângulo de reflexão, então o ângulo total do sistema pode ser representado como ou , então:
(1)
DITO ISTO, vamos para a resolução, sigam- me os bons!
Passo 2
Para a letra (a), primeiramente, vamos lembrar que e possuem seus lados direito e esquerdos mutuamente perpendiculares, logo
Resolvendo para , temos:
(2)
Passo 3
Para a letra (b), utilizaremos a equação (2) e aplicaremos , em seguida substituiremos as variáveis pelos dados estabelecidos na questão:
(Tô com sono y necessito de carinho) UHU, questão feita, bem simples, bem sussa, bem de boas, É ISSO AÍ GAFANHOTO, bons estudos e até a próxima!
Resposta
a)
b)