Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 79

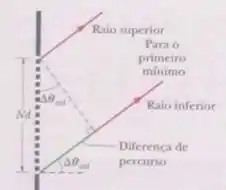
Uma rede de firação tem uma resolução . (a) Mostre que a diferença entre as frequências que podem ser resolvidas no limita da resolução, , é dada por . (b) Mostre que a diferença entre os tempos de percurso do raio de baixo e do raio de cima da figura é dada por . (c) Mostre que e, que, portanto, esse produto não depende dos parâmetros da rede. Suponha que .

Passo 1

(a) Vamos começar lembrando da relação entre a frequência e o comprimento de onda de uma onda de luz:

Para encontrar a relação entre uma “faixa de frequências” e uma “faixa de comprimentos de onda”, vamos derivar essa função em relação a :

Que pode ser escrita, em forma aproximada, de um outro jeito:

Agora vamos pegar a igualdade que foi dada no enunciado (aproximando ):

Juntando as duas expressões:

E já que estamos interessados apenas na diferença entre as frequências, podemos ignorar o sinal negativo:

Passo 2

(b) Se a diferença entre os caminhos percorridos pelos dois raios é , e eles se propagam com velocidade , a diferença no tempo de percurso entre os dois é:

Agora precisamos calcular essa diferença de caminho. Vamos fazer um desenho para ajudar:

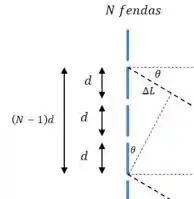
Então:

Como estamos falando de uma rede de difração, o número de fendas deve ser muito grande, então :

Passo 3

Então:

Mas nós sabemos que , então:

Resposta

(a) Demonstração.

(b) Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As cores de muitas asas de borboletas e carapaças de besouros são devidas a efeitos de difração. A borboleta Morfo tem elementos estruturais nas suas asas que efetivamente atuam como uma rede de difra

O espectro do neon é excepcionalmente rico na região do visível. Entre as muitas linhas há duas com comprimentos de onda de 519.313n m e 519.322 nm. Se a luz de um tubo de descarga de neônio incide no

Uma rede de difração que tem 4800 linhas por centímetro e é iluminada com incidência normal usando luz branca (intervalo de comprimento de onda de 400n m e 700n m ). Quantas ordens do espectro complet

Uma rede de difração tem n linhas por unidade de comprimento. Mostre que a separação angular ( ∆ θ ) entre duas linhas de comprimentos de onda λ e λ + ∆ λ é aproximadamente ∆ θ = ∆ λ 1 n 2 m 2 - λ 2 ,

O mercúrio tem vários isótopos estáveis, dentre os quais estão o H g196 e o H g202 . O intenso espectro de linhas do mercúrio em aproximadamente 546.07n m é uma composição de linhas espectrais dos vár