Uma máquina, usando de um gás ideal, inicialmente em um volume de e a uma temperatura de , realiza um ciclo que consiste em quatro etapas: (1) uma expansão isotérmica à temperatura de , até o dobro de seu volume inicial, (2) um resfriamento, a volume constante, até a temperatura de , (3) uma compressão isotérmica até seu volume original, e (4) um aquecimento, a volume constante, até sua temperatura original de . Considere . Esboce o ciclo em um diagrama e determine o seu rendimento.
Passo 1
A primeira coisa que a gente tem que fazer é desenhar o gráfico ! Vai ficar assim, ó:
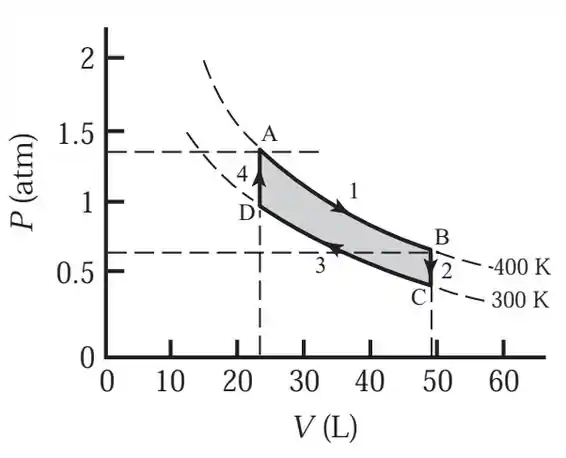
Passo 2
A gente quer a eficiência do sistema, ou seja, o rendimento da máquina térmica, ou seja, o trabalho do sistema sobre os calores quentes.
Agora vamos refletir um pouco sobre a fórmula aí de cima. Tá vendo que e são isovolumétricas? Então não tem trabalho nesses dois processos. Beleza! Agora vamos ver quais calores são quentes. Em , não tem trabalho e a energia interna aumenta, já que a temperatura aumenta. Daí pela primeira lei, a gente vê que o calor em é quente. No processo , o gás realiza trabalho (ou seja, ) e a energia interna não muda, então pela primeira lei, o calor de é quente. Show! Então a equação do rendimento fica:
Passo 3
Bom, agora a gente parte pra conta! O trabalho na isotérmica é , e e são isotérmicas, olha só que coincidência!
Então:
Agora vamos pros calores!
Pro processo :
Pro processo , que é isovolumétrico:
O nosso rendimento então vai ser:
Passo 4
Agora vamos mexer nos valores que temos do enunciado:
Divindo em cima e embaixo por :