Pequenos blocos, todos com a mesma massa , estão presos às extremidades e ao centro de uma barra leve de comprimento igual a . Calcule o momento de inércia do sistema em relação a um eixo perpendicular à barra passando a) pelo centro da barra e b) por um ponto a um quarto do comprimento a partir de uma das extremidades.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o momento de inércia do sistema em relação a um eixo perpendicular à barra para diferentes configurações.
Nós sabemos que o momento de inércia de um corpo de massa que está a uma distância do eixo de rotação é dado por:
Temos uma barra de comprimento , porém sua massa é leve, então neste caso, para o cálculo de momento de inércia iremos desprezar a massa desta barra.
Temos ainda três blocos de massas iguais , um em cada extremidade e o terceiro no centro da barra.
Agora que entendemos o que está acontecendo vamos aplicar a equação para o cálculo do momento de inércia em cada situação!
Passo 2
-
Aqui temos o caso do eixo passando pelo centro O da barra. A figura a seguir ilustra o sistema:
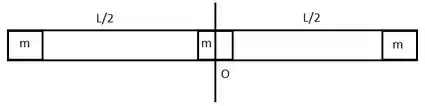
- Neste caso, temos o caso do eixo passando a ¼ de uma das extremidades da barra. A figura a seguir ilustra o sistema:
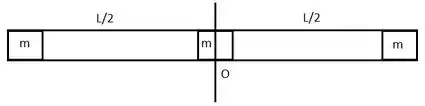
Podemos considerar os blocos, massas puntiformes neste caso. Os que se encontram nas extremidades da borda estão a uma distância do eixo, o que está no centro sua distância do eixo é . Portanto o momento de inércia será dado pela soma do momento de inércia de cada bloco em relação ao eixo que coincide com :
Passo 3
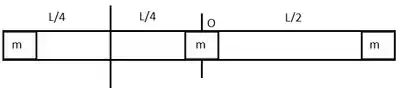
Como discutido no item a), os blocos são considerados massas puntiformes neste caso. O primeiro e o segundo se encontram a uma distância do eixo, o terceiro, que está na outra extremidade, está a uma distância . Portanto o momento de inércia será dado pela soma do momento de inércia de cada bloco em relação ao eixo.
Prontinho, galera! Até a próxima! 😉
Resposta
a)
b)