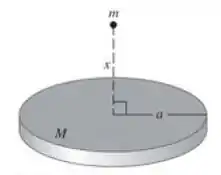
A massa está uniformemente distribuída ao longo de um disco de raio . Determine o módulo, a direção e o sentido da força gravitacional entre o disco e a partícula localizada a uma distância acima do centro do disco (Figura ). O seu resultado se reduz a uma expressão correta quando assume valores muito elevados? (Sugestão: divida o disco em anéis finos concêntricos infinitesimais; a seguir, use a expressão deduzida no Problema para a força gravitacional de cada anel e integre o resultado para achar a força total.)

A distância dessa massa até um ponto do anel externo é certo?

Então a força que uma massinha na ponta de fora desse anel vai ser assim:

Mas isso ao longo de todo anel. Então temos que ver se alguma componente vai ser cancelada. Pra isso, vou fazer um desenho, saca só:

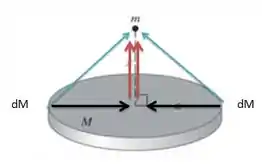A componente da força que vai contribuir é a em vermelha no desenho, já a preta vai se cancelar.

E assumindo que o ângulo entre o vetor azul (força gravitacional) e a distância vertical seja , a componente vertical ali em vermelho vai ir com o cosseno desse ângulo. E cosseno é o cateto adjacente sobre a hipotenusa, né? Então a contribuição da força na integral vai ser a seguinte:

O fator é por causa das duas componentes ali, tá?

Daí o diferencial de força vai ficar assim:

Agora é só integrar por todo comprimento de que vai de até o raio externo :

Agora consultando a tabela de integrais no fim do livro, temos o valor dessa belezinha aí:

E colocando em evidência pra cancelar com aquele ali no numerador ficamos com a seguinte expressão:

E o sentido/direção é vertical para cima na direção da massa .

E para , , e a força fica assim:

Como deveria ser!!