Exercícios de Força e Campo Gravitacional Envolvendo Integrais - Lista de Exercícios Resolvida
Questão 1
Determine a magnitude do campo gravitacional a uma distância de uma barra fina e homogênea de comprimento infinito, cuja massa por unidade de comprimento é .
Ver solução completaQuestão 2
Uma barra fina e homogênea de , com de comprimento, é dobrada em um semicírculo. Qual é a força gravitacional exercida pela barra sobre uma massa pontual de localizada no centro de curvatura do arco circular?
Ver solução completaQuestão 3
Uma esfera homogênea de massa está localizada próximo a uma barra fina e homogênea de massa e comprimento , como na Figura 11-31. Determine a força gravitacional de atração exercida pela esfera sobre a barra.

Questão 4
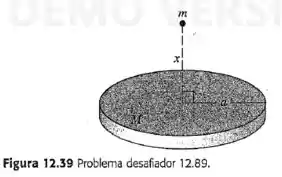
A massa está uniformemente distribuída ao longo de um disco de raio . Determine o módulo, a direção e o sentido da força gravitacional entre o disco e a partícula de massa localizada a uma distância acima do centro do disco (Figura 12-39). O seu resultado se reduz a uma expressão correta quando assume valores muito elevados? (Sugestão: Divida o disco em anéis finos concêntricos infinitesimais; a seguir, integre o resultado para achar a força total.)
Questão 5
A figura abaixo representa um anel delgado de raio e massa homogênea e uma massa pontual que está situada no eixo que passa pelo centro do anel a uma distância do mesmo. Dois elementos infinitesimais de massa do anel, diametralmente opostos, são ilustrados na figura.
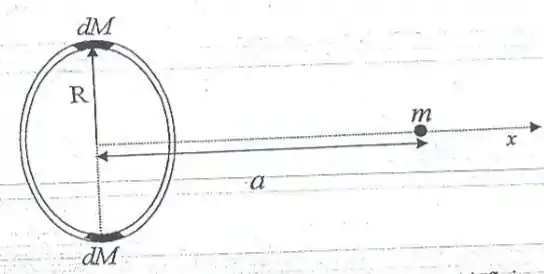
(a) Calcule o módulo da força resultante gravitacional infinitesimal que atua sobre a massa pontual devido à presença das massas infinitesimais .
(b) Qual é o módulo da força gravitacional resultante sofrida pela massa pontual devido, agora, à presença de todo o anel?
(c) Obtenha o módulo da força gravitacional para e para .
Ver solução completaQuestão 6
A figura abaixo representa um anel delgado de raio e massa homogênea e uma massa pontual que está situada no eixo que passa pelo centro do anel a uma distância do mesmo. Dois elementos infinitesimais de massa do anel, diametralmente opostos, são ilustrados na figura.
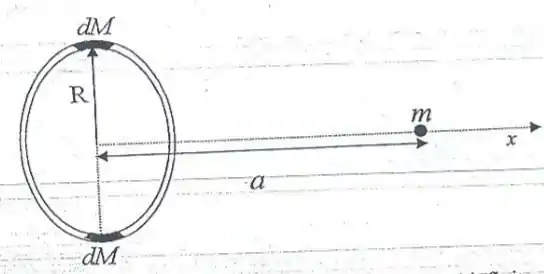
(a) Calcule o módulo da força resultante gravitacional infinitesimal que atua sobre a massa pontual devido à presença das massas infinitesimais .
(b) Qual é o módulo da força gravitacional resultante sofrida pela massa pontual devido, agora, à presença de todo o anel?
(c) Obtenha o módulo da força gravitacional para e para .
Ver solução completaQuestão 7
A figura abaixo mostra uma massa pontual situada no ponto e uma barra de massa e comprimento . A barra está situada a uma distância da massa pontual e sua densidade linear de massa é variável, dada por onde constante para .
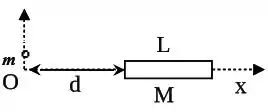
(a) Qual a força gravitacional resultante (módulo, direção e sentido) provocada pela barra sobre a massa ?
(b) Qual o valor da constante para que a Lei da Gravitação Universal de Newton seja recuperado no limite ?
Ver solução completaQuestão 8
A figura abaixo representa um semicírculo delgado de raio e massa homogênea e uma massa pontual que está situada centro do semicírculo. Dois elementos infinitesimais de massa , situados em ponto, para qual o raio forma um ângulo em relação ao eixo- que passa pelo centro do semicírculo, com ilustrado na figura:
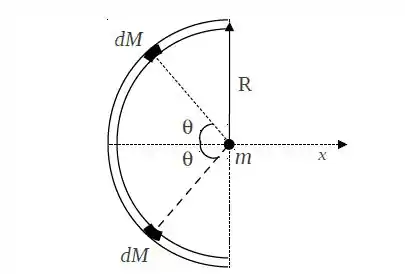
- Calcule o módulo da força gravitacional resultante que atua sobre a massa pontual devido à presença das massas infinitesimais
- Qual é o módulo da força gravitacional sofrida pela massa pontual devido, agora, à presença de todo o semicírculo.
- Usando o resultado do item b, obtenha qual seria a força sofrida pela massa no centro de um círculo completo.