Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Problemas - Ex. 82
Um fio uniforme de comprimento L e massa M está curvado em semicírculo. Calcule o módulo, direção e sentido da força gravitacional que o fio exerce sobre uma prticula de massa m situada no centro da curvatura do semicírculo.
Passo 1
E aí galera, vamos utilizar a equação
para calcular a força entre a massa do ponto e um pequeno segmento do semicírculo.
O raio do semicírculo é
Passo 2
Vamos dividir o semicírculo em pequenos segmentos de comprimento , como mostra a Figura a seguir:
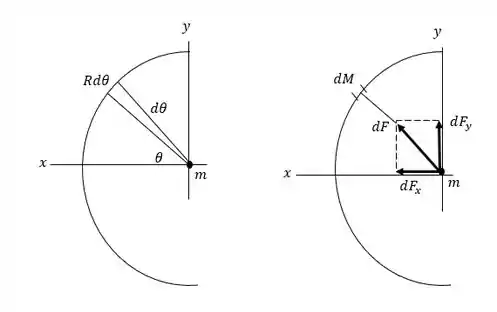
é a força da gravidade em exercida por
os componentes da metade superior do semicírculo cancelam os componentes da metade inferior.
Os componentes estão todos na direção e todos são adicionados.
Passo 3
Se o semicírculo fosse substituído por uma massa pontual em , a força da gravidade seria . Isso é vezes maior que a força exercida pelo fio semicirclar. Para o semicírculo são os componentes que são adicionados e a soma é menor do que se as magnitudes de força fossem adicionadas.