Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.3 - Ex. 30
Uma menina aplica uma força paralela ao eixo sobre um trenó de 10, que se desloca sobre a superfície congelada de um lago pequeno. À medida que ela controla a velocidade do trenó, o componente da força que ela aplica varia com a coordenada do modo indicado na Figura . Calcule o trabalho realizado pela força quando o trenó se desloca
a) de a ;
b) de a ;
Passo 1
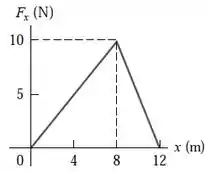
Opa, bora lá! O enunciado nos dá um gráfico de força versus comprimento e nos pede pra a gente calcular o trabalho em diferentes trechos:
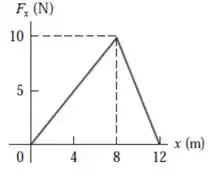
O trabalho realizado quando a força é variável pode ser dada de duas maneiras: ou integrando ou calculando a área do gráfico (que é nosso caso.) A ideia, aqui, é calcular a área embaixo de cada curva correspondendo ao deslocamento para cada item do problema.
A área de até representa um triângulo de base e altura , e sabemos que a área de um triângulo é base vezes altura dividido por dois! Tá quase no nosso DNA já! =D Agora é só aplicar:
Passo 2
Para o intervalo de deslocamento entre e também temos um triângulo, mas agora com base e altura . Aplicando na fórmula do triângulo:
Passo 3
Beleza até aqui? Certo! Agora, o problema pede o trabalho do ponto até o final . Bom, agora, é só somar os trabalhos calculados nos itens anteriores!
O trabalho total vai ser a soma dos dois outros trabalhos:
Ou calculando a área daquele triângulo grande de altura e base :
Dá no mesmo! Prontinho!