Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.3 - Ex. 20

Um microprocessador controla a posição do pára-choque dianteiro de um carro usado em um teste. A posição é dada por x t = 2,17 m + ( 4,80 m / s 2 ) t 2 - ( 0,100 m / s 6 ) t 6 .

a) Determine sua posição e aceleração para os instantes em que o carro possui velocidade zero.

b) Desenhe gráficos x t , v x t e a x t para o movimento do pára-choque entre t = 0 e t = 2,0   s .

Passo 1

Opa, bora resolver esse problema! Temos uma fórmula que relaciona a posição de um para-choque de um carro em função do tempo:

x t = 2,17 m + ( 4,80 m / s 2 ) t 2 - ( 0,100 m / s 6 ) t 6 .

A primeira coisa que ele pede é a sua posição e aceleração para os instantes em que o carro possui velocidade zero.

Aqui, nós precisamos calcular a derivada da função x ( t ) dada para encontrar a velocidade, v x .

E para que possamos encontrar a aceleração, a x , nós precisamos derivar novamente a função que já derivamos, ou seja, nós vamos derivar a função que encontramos para v x .

v x t = d x d t

E

a x t = d v x d t

Passo 2

  1. Então vamos começar derivando a função posição para encontrarmos a velocidade:

v x t = d 2,17 m + 4,80 m s 2 t 2 - 0,100 m s 6 t 6 d t = 9,60 m / s 2 t - ( 0,600 m / s 6 ) t 5

Agora vamos derivar a função v x t que encontramos para achar a aceleração:

a x t = d [ 9,60 m / s 2 t - ( 0,600 m / s 6 ) t 5 ] d t = 9,60 m / s 2 - ( 3 m / s 6 ) t 4

Passo 3

Então encontramos a posição x ( t ) e a aceleração a x t :

x t = 2,17 m + ( 4,80 m / s 2 ) t 2 - ( 0,100 m / s 6 ) t 6

a x t = 9,60 m / s 2 - ( 3 m / s 6 ) t 4

Quanto t = 0 :

x 0 = 2,17 m + ( 4,80 m / s 2 ) 0 2 - ( 0,100 m / s 6 ) 0 6

x = 2,17 m

E

a x 0 = 9,60 m / s 2 - ( 3 m / s 6 ) 0 4

a x = 9,60 m / s 2

Passo 4

Quanto t = 2 :

x 2 = 2,17 m + ( 4,80 m / s 2 ) ( 2 s ) 2 - ( 0,100 m / s 6 ) ( 2 s ) 6

x = 14,97 m

E

a x 2 = 9,60 m / s 2 - ( 3 m / s 6 ) ( 2 s ) 4

a x = - 38,4 m / s 2

Passo 5

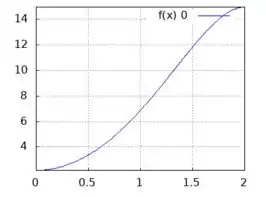
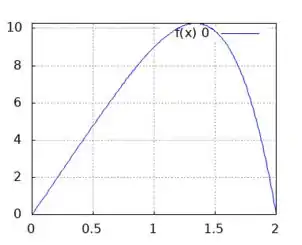
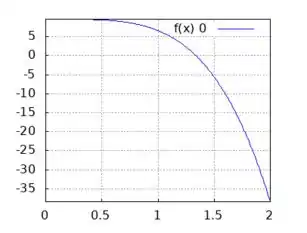
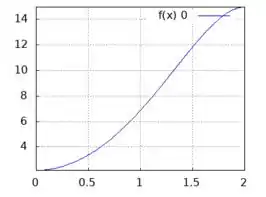
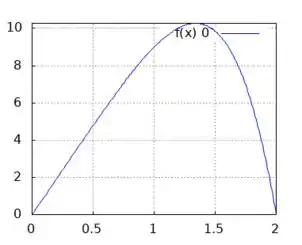
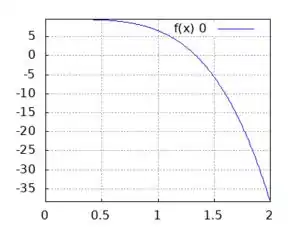
Usando uma calculadora gráfica ou outra ferramenta para desenhar os gráficos, eles ficam dessa forma:

x ( t ) :

v x ( t ) :

a x ( t ) :

Resposta

a)

x = 2,17 m

a x = 9,60 m / s 2

b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo do eixo x e tem sua posição descrita pela função x = ( 2 t 2 - t + 1 )m , onde t está em s. Em t = 2s , qual é (a) a posição, (b) a velocidade e (c) a aceleração da part
A FIGURA P 2.24 mostra o diagrama de movimento, feito a dois quadros de filme por segundo, de uma bola rolando em um trilho. Este possui um trecho pegajoso com de 3,0 m de comprimento. a. Use uma régu
A aceleração de uma partícula é descrita pela função a x = 10 - t m / s 2 , onde t está em s. Suas condições iniciais são x 0 e v 0 x 0m / s em t = 0 .a. Em que instante a velocidade volta a ser nula?
A velocidade de uma partícula é descrita pela função v x = k t 2m / s , onde k é uma constante e t está em s. A posição da partícula em t 0 = 0s é x 0 = - 9,0m . Em t 1 = 3,0s ela se encontra em x 1 =
Um bloco suspenso por uma mola é puxado para baixo e solto. O gráfico da posição versus tempo do bloco é mostrado na FIGURA P2.29. a. Em que instantes a velocidade é nula? Em que instantes ela é mais