Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 44
Um modelo de foguete se move no plano (o sentido positivo do eixo vertical é de baixo para cima). A aceleração do foguete possui os componentes e , onde , e . Para , o foguete está na origem e possui velocidade, sendo e .
a) Determine o vetor velocidade e o vetor posição em função do tempo.
b) Qual a altura máxima atingida pelo foguete?
c) Faça um desenho da trajetória do foguete.
d) Qual o deslocamento horizontal do foguete quando ele retorna para o ponto ?
Passo 1
E aí! como vai?
Nesse problema temos um foguete que se move no plano . A aceleração do foguete possui os componentes e , onde , e . Para , o foguete está na origem e possui velocidade, sendo e .
A partir daí queremos determinar o vetor velocidade e o vetor posição em função do tempo, a altura máxima atingida pelo foguete, um esquema da trajetória do foguete e qual o deslocamento horizontal do foguete quando ele retorna para o ponto .
Parece complicado?
Vamos começar definindo o vetor aceleração...
Certo? Veja só!
Passo 2
A aceleração é a derivada temporal da velocidade, então temos:
Se multiplicarmos por dos dois lados podemos integrar e assim achar uma expressão para a velocidade em função do tempo. A ideia vai ser semelhante para encontrar a posição. Mas daqui a pouco a gente vê isso. Primeiro vamos achar :
Substituindo os valores temos:
E como tinha falado antes, para determinar a posição em função do tempo, basta integrar novamente, isso porque ! Então integrando a velocidade para achar a posição vamos ter:
Daqui vão sair duas equações, uma pra posição de e outra pra :
Ajustando os valores teremos:
Tranquilo até aqui?
Passo 3
A altura máxima vai ser dada quando a velocidade na vertical é zero. A equação da velocidade na direção vertical é uma equação de segunda ordem e ela deve ser igual a zero:
Usando bhaskara achamos as raízes:
A raiz positiva vai nos dar o instante que queremos:
E a altura máxima é:
Bacana, não é?
Passo 4
As equações que descrevem a trajetória são:
E com a ajuda de um gerador gráfico podemos plotar :
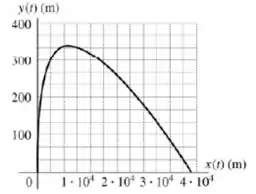
Show?
Passo 5
Para determinar o deslocamento horizontal, precisamos determinar quanto tempo o foguete leva para voltar ao solo, pois sua trajetória não é uma parábola simétrica. Fazendo na expressão para a posição vertical teremos:
Uma raiz é quando , o que faz sentido, pois o foguete parte da origem. Agora vamos as outras duas raízes. Usando bhaskara:
Colocando tudo isso na calculadora e descartando a raiz negativa:
E para esse valor de tempo, o deslocamento horizontal vai ser dado pelo nesse tempo. A expressão pra já temos, agora é só substituir:
E fim! Entendeu tudo? Responde Aí!
Resposta
