Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 16
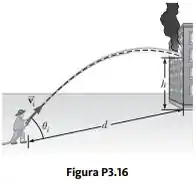
Um bombeiro, a uma distância de um edifício em chamas, direciona o jato de água de uma mangueira de incêndio a um ângulo acima da horizontal, como mostrado na Figura P3.16. Se a velocidade inicial do jato é , a que altura a água atinge o edifício?
Passo 1
Migos, aqui é um caso de lançamento oblíquo, ou seja, que não é nem 100% vertical, nem 100% horizontal.
Nesses casos em que dão pra gente a velocidade do lançamento e o ângulo que o objeto lançado faz com o solo (horizontal) a gente precisa fazer uma decomposiçãozinha desse vetor velocidade.
Guarda esse esqueminha no coração, vai usar muito! É assim, ó:
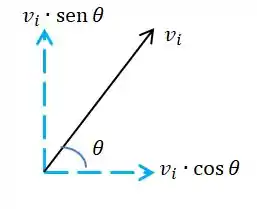
A gente sempre (sempre) vai dividir o movimento oblíquo do corpo/objeto/partícula nos movimentos vertical e horizontal, beleza?
Importante demais saber que o movimento vertical é acelerado, devido à gravidade, e isso vai fazer o objeto subir e descer.
Já o movimento na horizontal é uniforme: a velocidade é constante, sem aceleração – isso, claro, até o objeto cair!
Passo 2
Beleza. Considerando que a altura do prédio seja exatamente a altura máxima que a água atinge, pensa aqui comigo:
A altura máxima que o corpo (nesse caso a água) atingir vai ser o momento que ele vai ter velocidade vertical nula, certo?
Porque no momento que atinge essa altura ele começa a cair, e a gente já viu em exercícios de capítulos anteriores daqui da cinemática que o ápice da subida de um corpo ele tem velocidade zero!
Certo, mas, agora, direto ao ponto, como correlacionar as variáveis que a gente tem no enunciado, de modo a encontrar um a expressão pra ??
Passo 3
Vamos olhar só pro movimento na vertical agora, que é o que nos interessa. Ele é acelerado por conta da gravidade como falamos há pouco, certo?
Se a gente não tem dados de tempo do movimento, geralmente qual equação pra movimentos acelerados da cinemática a gente usa??
Claro, o famigerado Torricelli, olha ele aí:
Ok. Da fórmula a gente sabe que a velocidade final vai valer ;
Sabe que a velocidade (vertical!!) inicial, pelo esqueminha do Passo 1, vai valer ;
Sabe que a aceleração é exatamente a aceleração gravitacional, ou seja, ;
E sabe que, pra velocidade final valer zero, como a gente “impôs”, o deslocamento é exatamente a altura do prédio.
Então, gente, é só jogar na formulinha. E aqui a gente não vai usar valores numéricos, vai ficar tudo em função das letras mesmo, beleza?!
Passo 4
Finalmente, migos, a gente vai ter a seguinte expressãozinha:
Reparou que eu troquei o sinal do termo , né? Foi de pra porque a água está sendo jogada pra cima, e a gravidade se opõe a esse movimento. Portanto, pra não termos um valor negativo pra altura, a gente geralmente faz esse ajuste do sinal, ok?!
Voltando à expressão, vamos ter:
Certo?! Então é isso, gente, essa é a expressão pra altura do prédio em função da velocidade de lançamento da água e do ângulo que a água faz com a horizontal (o chão!).