Uma moeda de , com diâmetro de , rodopia a em torno de um eixo vertical. Ela rodopia sobre a borda, com seu centro diretamente acima do ponto de contato com a mesa. Olhando de cima, você vê a moeda rodopiar no sentido horário. (a) Qual é a quantidade de movimento angular (incluindo a orientação) da moeda em relação ao seu centro de massa? (Para o momento de inercia em relação ao eixo, veja a Tabela 9-1.) Trate a moeda como um cilindro de comprimento , no limite em que tende a zero. (b) Qual é a quantidade de movimento angular (incluindo a orientação) da moeda em relação a um ponto da mesa a do eixo? (c) Agora, o centro de massa da moeda se desloca sobre a mesa para o leste em uma linha reta, a , com a moeda rodopiando da mesma maneira que na parte (a). Qual é a quantidade de movimento angular (incluindo a orientação) da moeda em relação a um ponto da linha sobre a qual se desloca o centro de massa? (d) Deslizando e rodopiando, qual é a quantidade de movimento angular (incluindo a orientação) da moeda em relação a um ponto que está ao norte da linha sobre a qual se desloca o centro de massa?

(a) Nesse primeiro item queremos a quantidade de movimento angular em relação ao CM! Então podemos usar a fórmulinha

Usando :

Temos a velocidade angular em , precisamos passa-la para . Para isso, vamos multiplicar nossa velocidade por (o valor em radianos de cada revolução). Fica

Substituindo tudo na nossa fórmulinha

Fazendo a regra da mão direita para achar a orientação! Basta girar a mão no sentido horário (sentido que a moeda ta girando) e vemos que está entrando do plano do papel!

(b) Agora a nossa situação muda, porque queremos a quantidade de momento angular em um ponto fora da moeda. O continua o mesmo. Mas como estamos falando de um ponto externo, precisamos fazer

é o momento angular em relação ao eixo que passa pelo CM da moeda, ou seja, é o que a gente acabou de calcular na letra a). é o momento angular em relação ao eixo que passa pelo ponto dado. Ele tem essa fórmulinha:

Sendo que é a velocidade do centro de massa da moeda. Mas olha nossa situação. A moeda só gira em torno dela mesma. O seu CM não se mexe. Então temos que .

Assim . E nosso momento angular fica

A orientação também vai ser a mesma do item anterior, o vetor vai estar entrando na folha, já que a moeda continua girando no sentido horário.

(c) Essa é bem pareciada com a anterior, queremos o movimento angular em um ponto externo a moeda, então vamos usar

Mas agora o CM se mexe, então ele tem velocidade. Mas a olha nossa situação:

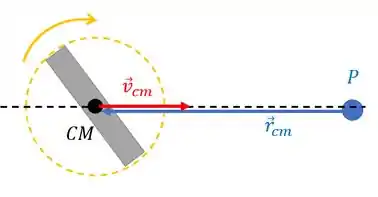
Lembra da fórmulinha

Esse vetor é o vetor que sai do ponto e vai até o CM da nossa moeda. Como o ponto está sobre a trajetória do CM da moeda, os vetores e estão na mesma direção. O que faz com que o produto vetorial zere. Assim, temos novamente .

Dessa forma, nosso momento angular fica igual ao do item a) novamente

Para acharmos a orientação, basta fazermos a regra da mão direita! Rodando no sentido horário, vemos que o vetor está entrando no papel!

(d) Agora nosso ponto não está mais sobre a linha do centro de massa!! Temos a situação:

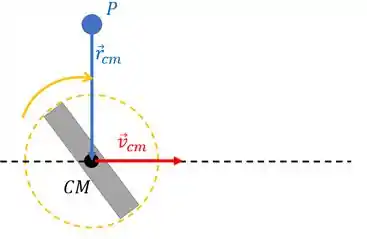
Vamos usar

Para o

Percebe no desenho que o ângulo entre os dois vetores é de , então o módulo desse produto vetorial pode ser calculado por

Sendo a distância entre o ponto e o CM. Calculando

Mas repara que em relação ao eixo que passa pelo CM, a moeda gira no sentido horário, mas em relação ao ponto , ela vai girar no sentido anti-horário, por causa do sentido da velocidade. Sendo assim, e vão ter sentidos opostos. Logo, sinais opostos.

Vamos considerar que o sentido horário é o positivo, assim, temos que

A quantidade de momento angular total é

O ficou negativo porque ele está no sentido anti-horário.

Calculando

Esse sinal de menos indica que estamos no sentido inverso ao sentido horário, logo no anti-horário. Usando a regra da mão direita no sentido anti-horário, o vetor está apontando para gente, isto é, saindo do plano do papel.

Obs: Ficamos diferente do gabarito nesse ultimo item, mas acreditamos que há um errinho no gabarito, ok? Por ele não considerar que os momentos angulares estão em sentidos opostos.