Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 38
Você observa uma partícula de se movendo com uma rapidez constante de no sentido horário em torno de um círculo de de raio. (a) Qual é a quantidade de movimento angular da partícula (incluindo a orientação) em relação ao centro do círculo? (b) Qual o momento de inércia da partícula em relação a um eixo que passa perpendicularmente ao plano do centro do círculo? (c) Qual é a velocidade angular da partícula?
Passo 1
a) Nessa questão ele pede pra gente calcular a quantidade de movimento angular de uma partícula que está fazendo um movimento circular com velocidade constante. Os dados são
Aqui, podemos lembrar que o momento angular é dado por
E lembrar também que isso pode ser escrito na forma escalar:
Onde é o ângulo entre o vetor velocidade (que tem a mesma direção e sentido de e , qe é o vetor que sai do centro do círculo e vai até a partícula.
A ideia é a gente usar essa fórmulinha para calcular o que ele pede. E depois vamos usar a regra da mão direita pra ver a orienteção desse momento angular!
Passo 2
Temos todos os dados para usar essa fórmulinha:
Só falta , né? Olha a nossa situação:
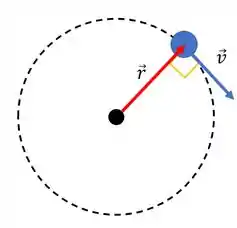
Como temos um movimento circular, a velocidade é tangente ao círculo, logo o ângulo entre a velocidade e o vetor é . Assim a gente está preparado para usar a fórmulinha!
Logo,
Pela regra da mão direita: nossos dedos devem girar no sentido do movimento (sentido horário como fala o enunciado), quando fazemos isso, nossos dedão entra no plano da folha.
Vemos então que o vetor está entrando no papel!
Passo 3
(b) Para o momento de inércia, temos a fórmulinha para o nossos caso, onde temos apenas uma partícula:
Logo,
Passo 4
(c) Pra finalizar, ele quer o
Não esquece: temos a fórmulinha . Vamos usar!
Assim, isolando
Resposta
entrando no plano do papel
b)
c)