Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.5 - Ex. 49

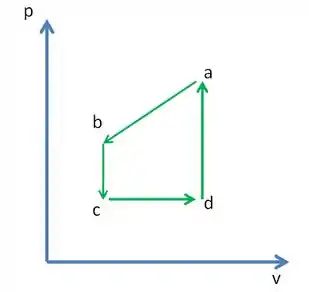
A figura mostra um ciclo fechado de um gás (a figura não foi desenhada em escala). A variação da energia interna do gás ao passar de para ao longo da trajetória é . Quando o gás passa de para , recebe na forma de calor . Mais são recebidos quando o gás passa de para . Qual é o trabalho realizado sobre o gás quando passa de para ?

Passo 1

Primeiro, vamos lembrar que, pela primeira lei da termodinâmica, que nos demonstra a conservação da energia, temos:

Como em um ciclo a variação de energia interna é sempre nula, temos:

Passo 2

Beleza! Vamos, então, trabalhar com os dados do enunciado! Mas, antes disso, perceba que :

Ok! A primeira coisa que nos é dita é que e, então, com , vem:

, pois .

Passo 3

Agora, então, basta a gente trabalhar com a expressão anterior, pois o enunciado nos diz que e . Daí, temos:

e, então:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um mol de um gás ideal, contido num recipiente munido de um pistão móvel, inicialmente a 20 ° C , se expande isotermicamente até que seu volume aumenta de 50 % . A seguir, é contraído, mantendo a pres

Um mol de um gás ideal descreve o ciclo A B C D A representado na figura no plano ( P , V ) , onde T = T 1 e T = T 2 são isotermas. Calcule o trabalho total associado ao ciclo, em função de P 0 , V 0

Um mol de gás ideal, com γ = 7 / 5 , está ocntido num recipiente, inicialmente a 1a t m e 27 ° C . O gás é, sucessivamente: (i) comprimido isobaricamente até 3 / 4 do volume inicial V 0 ; (ii) aquecid

Um mol de um gás ideal, partindo das condições N T P , sofre: (i) uma compressão isotérmica até um volume é de 5l , seguida de (ii) uma expansão adiabática até retornar ao volume inicial, atingindo um

1l de H 2 (para o qual γ = 7 / 5 ), à pressão de 1 atm e temperatura de 27 ° C , é comprimido adiabaticamente até o volume de 0,5l e depois resfriado, a volume constante, até voltar à pressão inicial.