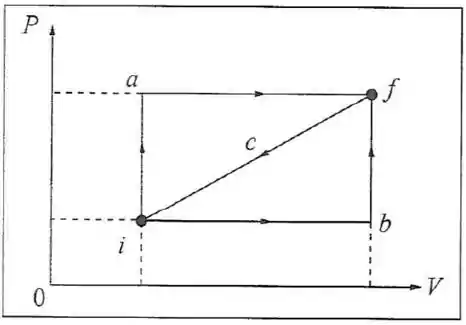
Um fluido homogêneo pode passar de um estado inicial a um estado final no plano através de dois caminhos diferentes, representados por e no diagrama indicador (figura). A diferença de energia interna entre os estados inicial e final . O trabalho realizado pelo sistema na passagem de para é de . O trabalho realizado pelo sistema quando descreve o ciclo () é de . A partir destes dados, determine, em magnitude e sinal: (a) a quantidade de calor , associada ao caminho ; (b) o trabalho ; (c) a quantidade de calor associada ao caminho ; (d) Se o sistema regressa do estado final ao estado inicial seguindo a diagonal do retangulo (figura), o trabalho e a quantidade de calor associados a esse caminho.
Passo 1
Fala galera, bora fazer mais um exercício?
(a) Vamos lembrar que, em um diagrama , a área sob uma curva é igual ao trabalho realizado pelo gás.
Então, quando o enunciado dá o trabalho realizado ao longo do trajeto , estamos falando dessa área:
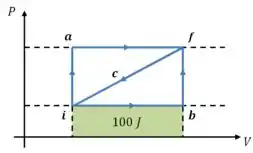
E o trabalho realizado no trajeto é nulo, já que o volume é constante nesse trecho.
Como a variação de energia interna entre e é , podemos usar a primeira lei da termodinâmica para resolver o problema:
Passo 2
(b) Agora queremos calcular o trabalho realizado entre .
Essa resposta depende do caminho escolhido entre os dois pontos (passando pelo ponto ou pelo ponto ). Pelo contexto, vamos supor que o enunciado está se referindo ao caminho .
Então nosso objetivo é calcular a seguinte área:
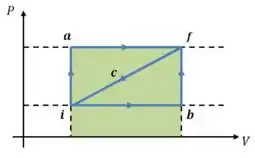
Nesse caso, começamos usando o fato de que o trabalho ao longo do ciclo completo é de , então:
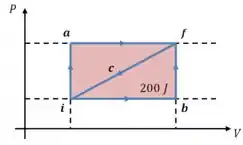
E que o trabalho realizado ao longo do trajeto é de , então:
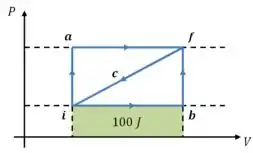
Só precisamos somar essas duas áreas para encontrar a área sob o trajeto :
Passo 3
(c) E agora queremos encontrar o calor . Podemos fazer isso usando a primeira lei da termodinâmica:
E já temos todos os valores necessários para essa conta:
Passo 4
(c) Se o sistema passa pela diagonal para voltar ao estado inicial, o trabalho realizado nesse processo equivale à seguinte área:
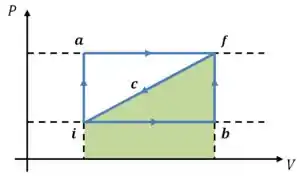
Aqui só precisamos inverter os sinais de duas áreas que nós já calculamos:
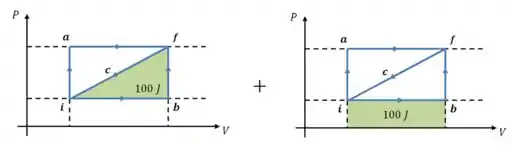
Então:
E o sinal de menos aparece porque o trajeto está no sentido da redução do volume do gás. Isso quer dizer que o trabalho está sendo realizado sobre o gás.
Passo 5
E para calcular a quantidade de calor nesse processo, podemos usar a primeira lei da termodinâmica mais uma vez.
(Se a diferença de energia interna é de , então o caminho contrário dá de variação.
Ou seja:
E o sinal negativo que o gás está rejeitando calor.
Resposta
(a) .
(b) .
(c) .
(d) e .