Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 38

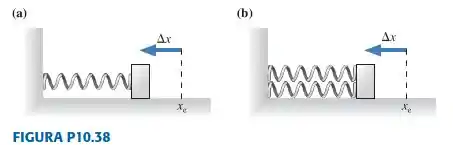
38. || A mola da FIGURA P10.38a é comprimida em . Ela lança o bloco com rapidez ao longo de uma superfície livre de atrito. As duas molas da FIGURA P10.38b são idênticas à mola da Figura P10.38a. Elas estão comprimidas no mesmo valor e são usadas para lançar o mesmo bloco. Qual será, agora, o módulo da velocidade do bloco?

Passo 1

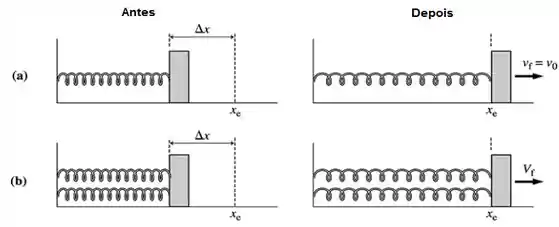
Um esquema é:

Passo 2

Podemos usar o principio de conservação de energia e já levar em conta o

No caso , teremos (Energia potencial elástica) sendo convertida em (Energia cinética)

Já no caso , teremos 2 molas idênticas então ficamos:

Fazendo a igualdade , com o que calculamos antes, fica:

Essa será a relação de velocidade final do bloco com a velocidade inicial, veja que não acha-se um valor numérico, e sim uma expressão nessa questão.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o cavaleiro do Exemplo 7.7 (Seção 7.2) e a Figura 7.16. Como no exemplo, o cavaleiro é libertado a partir do repouso quando a mola está esticada 0,100 m. Qual é o deslocamento x do cavaleiro

Um queijo de 1,20k g é colocado sobre uma mola de massa desprezível e constante k = 1800N / m que está comprimida 15,0c m . Até que altura acima da posição inicial o queijo se eleva, quando a mola é l

a) Para o elevador do Exemplo 7.9 (Seção 7.2), qual era a velocidade do elevador quando ele desceu 1,0 m a partir do ponto 1 da Figura 7.17? b) Quando o elevador desceu 1,0 m a partir do ponto 1 da Fi

Considere o cavaleiro do Exemplo 7.7 (Seção 7.2) e a Figura 7.16. a) Como no exemplo, o cavaleiro é libertado a partir do repouso quando a mola está esticada 0,100 m. Qual é a velocidade do cavaleiro

Você foi solicitado para projetar uma mola que deve fornecer a um satélite de 1160k g uma velocidade de 2,50m / s em relação a uma estação espacial em órbita. Sua mola deve fornecer ao satélite uma ac