Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.2 - Ex. 24

a) Para o elevador do Exemplo 7.9 (Seção 7.2), qual era a velocidade do elevador quando ele desceu 1,0 m a partir do ponto 1 da Figura 7.17? b) Quando o elevador desceu 1,0 m a partir do ponto 1 da Figura 7.17, qual era sua aceleração?

Passo 1

Nós vamos usar os métodos de energia.

A energia potencial elástica e gravitacional mudam.

O trabalho é feito por atrito.

Vamos escolher o ponto 1 e tomar como essa a origem, então y 1 = 0 .

Seja o ponto 2 1 m abaixo do ponto 1, então: y 2 = - 1 m .

Passo 2

  1. Então, vamos aplicar:

    2. K 1 + U 1 + W = K 2 + U   2

    Sabemos que:

    K 1 = 1 2 m v 1 2 = 1 2 ⋅ 2000 k g ⋅ 25 m s 2 = 625,00 J

    E U 1 = 0 .

    Passo 3

    Vamos, agora, calcular W :

    W = - f y 2 = - 17,000 N ⋅ q m = - 17,000 J

    Passo 4

    Sabemos que:

    K 2 = 1 2 m g 2 2

    E então:

    U 2 = U g r a v , 2 + U e l , 2 = m g y 2 + 1 2 k y 2 2

    Assim,

    U 2 = 2000 k g ⋅ 9,8 m s 2 ⋅ - 1 m + 1 2 ⋅ 1,41 × 10 5 N m ⋅ 1 m 2

    U 2 = - 19,600 J + 70,500 J = + 50,900 J

    Então,

    625,000 J - 17,00 J = 1 2 m v 2 2 + 50,900 J

    1 2 m v 2 2 = 557,100 J

    Isso implica que:

    v 2 = 2 ⋅ 557,100 J 2000 k g = 23,6 m / s

    O elevador para após descer 3 m . Depois de descer 1 m , ainda está em movimento, mas

    abrandou.

    Passo 5

  2. Vamos aplicar a segunda lei de Newton para o elevador: ∑ F y = m a y . Como conhecemos as forças, podemos resolver para encontrarmos a aceleração.

Primeiro, vamos esboçar um diagrama de corpo livre para o elevador:

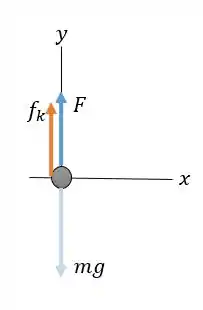
Temos que:

F   =   k d

onde d é a distância que a mola é comprimida.

Então, aplica a segunda lei de Newton:

∑ F y = m a y

f k + F - m g = m a

f k + k d - m g = m a

Isso implica que:

a = f k + k d - m g m = 17,000 N + 1,41 × 10 5 N m ⋅ 1 m - 2000 k g ⋅ 9,8 m / s 2 2000 k g = 69,2 m / s 2

Calculamos que a é positivo, então a aceleração é para cima.

Resposta

  1. v 2 = 23,6 m / s
  2. a = 69,2 m / s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29 . | A F I G U R AE X 10.29 é o diagrama de energia potencial para uma partícula de 20g que é liberada do repouso em x =1,0m . a . A partícula se moverá para a direita ou para a esquerda? Como você
32 . || a. Na F I G U R AE X 10.32 , qual é o valor mínimo de velocidade que uma partícula de 100g necessita ter no ponto A para poder chegar ao ponto B ? b . Qual é o mínimo valor de velocidade que u
44 . ||| Um cofre de 1.000k g encontra-se 2,0m acima de uma mola dura e resistente quando o cabo que o sustenta se rompe. O cofre colide com a mola e a comprime em 50c m . Qual é a constante elástica
47 . || Uma panela de massa desprezível está suspensa por uma mola presa ao teto. Quando vazia, a panela fica parada a 50c m abaixo do teto. Se um punhado de 100g de argila é suavemente colocado na pa
39 . || A mola da F I G U R AP 10.39 a é comprimida em Δ x . Ela lança o bloco ao longo de uma superfície sem atrito com velocidade v 0 . As duas molas da FIGURA P10.39b são idênticas à da F i g u r a