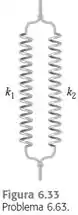
Molas em paralelo. Duas molas são consideradas em paralelo quando uma está paralela em relação à outra e elas estão ligadas pelas extremidades (Figura 6.33). Podemos considerar que essa combinação equivale a uma única mola. A constante de força da mola única equivalente é chamada de constante de força efetiva, , da combinação.

a) Demonstre que a constante de força efetiva dessa combinação é .

b) Generalize esse resultado para molas em paralelo.

Opa, bora resolver esse problema! Aqui temos duas molas ligadas pela extremidade e em paralelo. Assim:

O enunciado diz que a gente pode considerar que essa combinação equivale a uma mola de constante

Para a letra (a) temos que provar que:

Considerando a figura do problema, a força que é aplicada no sistema, diretamente no nó podemos chamar de e ela se distribui entre as duas molas em e de modo que:

Como a expressão pra força elástica é e o deslocamento nas duas molas é o mesmo, pois a força aplicada é no nó, então as duas se esticam ou se comprimem igualmente, podemos reescrever a expressão da soma das forças assim ó:

Dividindo tudo por :

Uma já foi!