Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 67
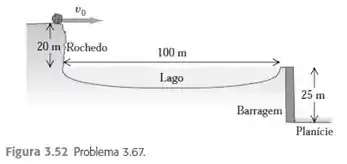
Uma rocha de rola horizontalmente pelo topo de um rochedo vertical, que está acima da superfície de um lago, conforme a Figura . O topo da face vertical de uma barragem localiza-se a do pé do rochedo, sendo que o topo da barragem está no mesmo nível da superfície do lago. Uma planície nivelada está abaixo do topo da barragem.
a) Qual deve ser a velocidade mínima da rocha ao cair do rochedo, de modo que role para a planície, sem atingir a represa?
b) A que distância da base da represa a rocha atinge a planície?
Passo 1
Oi, galerinha! Tudo bom?
Primeiro, vamos entender o que está acontecendo. Temos uma rocha que vai sair do rochedo com apenas velocidade horizontal . Então, o enunciado quer saber o valor mínimo dessa velocidade para a rocha não encostar e ficar na parede da barragem, mas sim cair direto na planície. Um esqueminha:
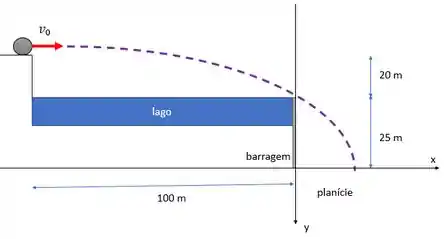
Vamos assumir que o eixo vertical seja positivo apontando para baixo. As condições iniciais do problema são:
Certo?
Passo 2
- Agora vamos usar as equações do movimento vertical para determinar o instante que a pedra chega no nível do lago em , após sair de (lembrando que o eixo está para baixo, por isso as coordenadas negativas).
- Agora queremos saber a que distância a pedra atinge. Aqui a ideia é usar as equações de movimento na vertical para achar o tempo de voo total, para depois com a equação para o movimento na horizontal, achar o deslocamento da pedra. Vamos lá?
Substituindo os valores:
Assim a pedra deve viajar horizontalmente uma distância de durante para não cair antes da parede fina da barragem. A velocidade horizontal vai ser:
Show?
Passo 3
Ela deve viajar, ao todo, do topo do rochedo até a planície. Usando a equação de movimento que usamos no item anterior:
Vemos que a pedra levou para atingir o solo, e mais s para chegar na planície.
Agora usando a equação do horizontal teremos a distância da barragem até o ponto onde a rocha chega no solo, e admitindo que a origem é a barragem e, portanto a posição inicial da pedra era :
Assim a pedra cai a uma posição depois da barragem.
E aí! entendeu tudo? Responde Aí!
