Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 49
A molécula de metano ( possui quatro átomos de hidrogênio localizados nos vértices de um tetraedro regular de de lado, com o átomo de carbono no centro do tetraedro (figura 9-48). Determine o momento de inércia desta molécula para rotações em torno de um eixo que passa pelos centros do átomo de carbo e de um dos átomos de hidrogênio.
Passo 1
Falaaa, querido! Cê está bem?
Então, ele quer o momento de inércia dessa molécula em relação a um eixo que passe, ao mesmo tempo, pelo centro da molécula de carbono (a do centro) e por uma molécula de hidrogênio. E esses hidrogênios estão nos vértices de um tetraedro. Então fica algo assim:
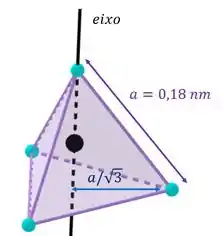
O momento de inércia desse sistema vai ser a soma do momento de inércia de cada partícula dele. Então a gente precisa calcular o momento de inércia de cada átomo desse em relação a esse eixo preto.
Bem esses átomos são partículas mesmo. O momento de inércia de uma partícula em relação a um eixo é dado por
Onde é a massa da partícula (aí a gente vai precisar olhar no apêndice C as massas do átomo de hidrogênio e carbono). E é a distância da partícula até o eixo em questão. Isso a gente descobre usando geometria espacial.
Fica tranquilo se não lembrar muito de geometria espacial, a gente vai se ajudando, tá? Bora lá!
Passo 2
Percebe que o eixo passa através do centro da base do tetraedro.
O átomo de carbono e o átomo de hidrogênio no vértice superior do tetraedro não contribuem para o momento de inércia, pois seus núcleos estão sobre o eixo, e assim a distância deles até o eixo é nula.
Então, só os três átomos de hidrogênio vão ter momento, os vértices da base. Da geometria espacial, esses átomos estão a uma distância do centro da base do tetraedro (por onde o eixo passa), onde é a medida do lado do tetraedro, que o enunciado diz que vale:
Assim, para esses 3 átomos hidrogênio, teremos
E assim o momento de inércia de um deles vai ser:
Passo 3
Como temos 3 átomos de hidrogênio contribuindo para o momento de inércia do sistema, vamos ter:
Substituindo a nossa expressão de :
Substituindo valores, vendo no apêndice C que :