Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 48
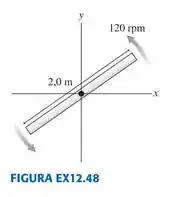
48. Qual é o momentum angular da haste de em rotação mostrada na FIGURA EX12.48?
Passo 1
O momento angular de um objeto simétrico girando sobre o centro de gravidade pode ser dado por...
Onde é o momento de inércia da barra dada pela tabela 12.2 do capítulo...
OBS: No livro, a tabela menciona o comprimento como , mas aqui, não vamos utilizar isso, pois para nós já é o momento angular que estamos buscando .
Onde no nosso caso, no nosso caso é , e a massa... .
A única coisa que precisamos encontrar então é a velocidade angular! Vamos nessa?
Passo 2
POXA! O desenho já nos dá a velocidade angular, todavia está em . Logo, devemos converter para , o que pode ser feito facilmente multiplicando o valor por :
Logo...
O sentido do momento é dado pela regra da mão direita, que no nosso caso é saindo da tela, já que a haste gira no sentido anti-horário.
Resposta
Sentido saindo da tela.