Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 52

52. Um triângulo equilátero com 5,0   c m de lado gira em torno de seu centro de massa a 120   r p m . Quanto vale a velocidade de um vértice do triângulo?

Passo 1

Primeiro, vamos desenhar esse triângulo para termos uma noção geométrica do problema:

Todo o triângulo gira com velocidade angular constante de 120   r p m . A velocidade de um dos vértices pedidas no problema é a velocidade normal, em m / s . Essa velocidade pode ser obtida para um dos pontos pela equação:

v = R ω

Onde R é a distância de um dos lados do triângulo até o centro (que também é o centro de rotação).

Passo 2

Para um triângulo equilátero...

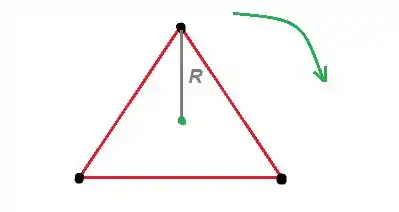
O Raio, vale 2 / 3 da altura h :

R = 2 3 h

E a altura pode ser encontrada por Pitágoras, já que ele forma um cateto e o outro é a metade do lado desse triângulo...

h 2 + a 2 2 = a 2       →

h 2 = a 2 - a 2 4 = 3 a 2 4

Então a altura vale em termos do lado...

h = a 2 3

E, portanto...

R = 2 3 h = 3 3 L

Como no nosso caso o lado vale 5   c m ou 0,05 m ...

R = 0,029   m

A velocidade de um dos pontos então será...

v = R ω = 0,029 ⋅ 120 ⋅ 2 π 60   m / s

O motivo de estarmos multiplicando por 2 π 60 é para transformar a velocidade angular que está em r p m para r a d / s (unidade padrão no SI):

v = 0,36   m / s

Resposta

v = 0,36   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 10-33 mostra um arranjo de 15 discos iguais colados para formar uma barra de comprimento L=1,0000m e massa total M=100,0m g . O arranjo pode girar em tomo de um eixo perpendicular que passa pel
A Terra, que não é uma esfera uniforme, possui momento de inércia igual a 0.3308 M R 2 em relação a um eixo ligando o pólo norte ao pólo sul. O tempo para a Terra completar um giro é igual a 86164 s.
Os três objetos uniformes indicados na Figura 9.23 possuem a mesma massa m. O objeto A é um cilindro maciço de raio R . O objeto B é uma casca cilíndrica de raio R . O objeto C éum cubo maciço cuja ar
Uma batuta consiste em um fino cilindro metálico de massa M e comprimento L. Cada extremidade possui uma tampa de borracha de massa m, e cada tampa pode ser tratada com precisão como uma partícula nes
Um volante de motor a gasolina deve fornecer uma energia cinética igual a 500J, quando sua velocidade angular diminui de 650 rev/min para 520 rev/min. Qual é o momento de inércia necessário?