Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 48
Mostre que o campo elétrico devido a uma fina casca cilíndrica, infinitamente longa e uniformemente carregada, com raio e densidade superficial de carga , é dado pelas seguintes expressões: para e para
Passo 1
Fala ai galera, mais uma questão que devemos aplicar a lei de Gauss. Sabemos que
Como a simetria do problema é cilíndrica, nada melhor do que fazermos uma Gaussiana cilíndrica, né?!
Passo 2
- Consideremos o caso .
- Consideremos o caso .
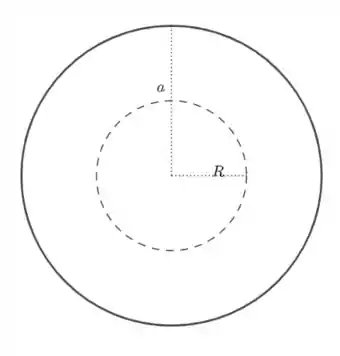
Nesse caso, temos . Dessa maneira, pela lei de Gauss, concluímos que .
Passo 3
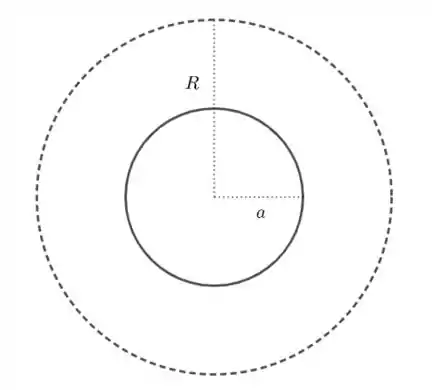
Nesse caso, temos
onde é o comprimento do cilindro. Assim, pela lei de Gauss, temos
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um antigo modelo atômico, proposto por Rutherford logo após sua descoberta do núcleo atômico, era constituído por uma carga puntiforme positiva + Z e (o núcleo) no centro de uma esfera de raio R com c
Uma casca esférica tem raio interno R i n t e raio externo R e x t . A casca contém carga total Q, uniformemente distribuída. O interior da casca não contém carga nem matéria.a. Determine o campo elét
Todos os exemplos da lei de Gauss usaram superfícies altamente simétricas através das quais a integral de fluxo é nula ou igual a E A . Nós também alegamos que o fluxo resultante Φ e = Q i n t ε 0 é i
Um cilindro infinito longo e de raio R apresenta uma densidade linear de carga λ . A densidade volumétrica de carga (em C / m 3 ) no interior do cilindro ( r ≤ R ) é dada por ρ r = r ρ 0 / R , onde p
A intensidade do campo elétrico a 2,0c m da superfície de uma esfera metálica com 10c m de diâmetro é de 50.000N C . Qual é a carga (em n C ) da esfera?