Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 42

Uma esfera sólida não condutora de raio R tem uma densidade volumétrica de arga que é proporcional à distância ao centro. Ou seja, ρ = A r para r ≤ R , onde A é uma constante. (a) Determine a carga total na esfera. (b) Determine as expressões para o campo elétrico no interior da esfera ( r < R ) e fora da esfera ( r > R ). (c) representa a magnitude do campo elétrico como uma função da distância r ao centro da esfera.

Passo 1

Falaa galera, tudo tranquilo? Então, temos um problema em que a densidade de carga em uma esfera não é uniforme, mas muda com o raio! Assim, não podemos simplesmente multiplicar a densidade pelo volume para obter a carga, blz? Acompanhe a resolução...

Passo 2

  1. Por definição, temos que

    2. q = ∫ ρ   d V

    onde a integração é feita ao longo de todo o volume da esfera. Notemos que podemos relacionar V com o raio r através da fórmula do volume de uma esfera:

    V = 4 3 π r 3

    Tomando as diferenciais dos dois lados, temos

    d V = 4 3 π 3 r 2 d r = 4 π r 2   d r

    onde usamos a regra do tombo para derivar r 3 . Dessa forma, segue que:

    q = ∫ A r 4 π r 2   d r = 4 π A ∫ 0 R r 3   d r

    Note que integramos de 0 até R . Isso garante que percorremos toda a esfera. Assim,

    q = π A R 4

    Passo 3

  2. Podemos usar a lei de Gauss para escrever:

    3. ∮ E → ⋅ d A → = q i n t ε 0

  • Para r < R :

    • A nossa superfície Gaussiana será uma esfera de raio r < R , como mostra a figura abaixo.

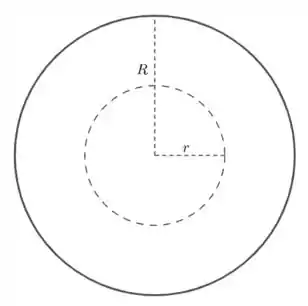
    Notemos que a carga em função do raio r é

    q i n t = π A r 4

    (basta substituir R por r na integral que usamos para calcular a carga no item (a)). Dessa forma,

    ∮ E → ⋅ d A → = π A r 4 ε 0 E ∮ d A = π A r 4 ε 0 E 4 π r 2 = π A r 4 ε 0 E = A 4 ε 0 r 2

  • Para r > R

A ideia aqui é a mesma. Temos q i n t = π A R 4 , de modo que

E 4 π r 2 = π A R 4 ε 0 E = A R 4 4 ε 0 r 2

Observe que as expressões são iguais quando r = R !!! Isso indica a continuidade de E em um material isolante. Legal, né?

Passo 3

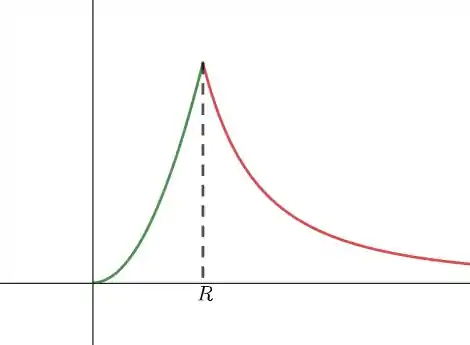
  • Abaixo representamos o gráfico que representa E em função de R .

    • Note que inicialmente o campo elétrico cresce; quando r = R ele começa a decrescer!

    Resposta

    1. π A R 4
    2. A r 2 / 4 ε 0 e A R 4 / 4 ε 0 r 2
    3. Veja a figura
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Uma bola esférica carregada tem um raio R e uma carga total Q. A intensidade do campo elétrico no interior da bola (para r ≤ R ) é dada pela expressão E r = E m a x r 4 R 4 .a. Qual é o E m a x em fun
    Um fio reto, longo e fino, com densidade linear de carga λ , passa pelo centro de um cilindro metálico fino e oco, de raio R. O cilindro possui uma densidade de carga linear líquida igual a 2 λ . Cons
    Uma esfera de raio R possui uma carga total Q. A densidade de carga volumétrica (em C / m 3 ) no interior da esfera é dada por ρ r = C / r 2 , onde C é uma constante a ser determinada.a. A carga no in
    Uma esfera de raio R possui uma carga total Q. A densidade de carga volumétrica (em C / m 3 ) no interior da esfera é dada por ρ = ρ 0 1 - r R Essa densidade de carga decresce linearmente desde o valo
    Uma placa infinita, carregada e de espessura 2 z 0 , é posicionada paralelamente ao plano x y , entre z = - z 0 e z = + z 0 . Sua densidade volumétrica de carga (em C / m 3 ) é uma constante.a. Use a