Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 133
(a) Mostre que, se o objeto O da Fig. 34-19c for deslocado do ponto focal F1 em direção ao olho do observador, a imagem se deslocará do infinito em direção à lente e o ângulo θ′ (e, portanto, a ampliação angular mθ) aumentará. (b) Se o processo continuar, em que ponto estará a imagem quando mθ atingir o maior valor que permite observar uma imagem nítida? (c) Mostre que esse valor máximo de mθ é 1 + (25 cm)/f. (d) Mostre que, nessa situação, a ampliação angular é igual à ampliação lateral.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vai ser tranquilo, vem comigo.
Letra a:
Neste caso , e a Eq. 34.9 do livro torna-se . Nós diferenciamos isso com relação ao tempo (t) para obter:
Conforme o objeto é movido em direção à lente, p está diminuindo, então . Consequentemente, a expressão acima mostra que ; ou seja, a imagem se move do infinito. A ampliação angular também aumenta conforme mostra o gráfico a seguir:
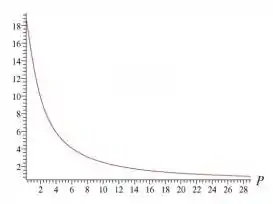
Para obter este gráfico de , escolhemos .
Passo 2
Letra b:
Quando a imagem parece estar no ponto próximo (ou seja, , está no seu valor máximo utilizável - uma vez que geralmente se considera igual a 25cm (este valor também foi usado para fazer o gráfico acima).
Passo 3
Letra c:
Nesse caso:
Se usarmos a aproximação de pequeno ângulo, teremos . Portanto, encontramos:
Que se torna:
Que facilmente simplifica para o resultado desejado.
Passo 4
Letra d:
A ampliação linear é dada por . Assim que definimos (ver parte (b)), então isso mostra a igualdade nas ampliações.
Resposta
- Gráfico
- Quando a imagem parece estar no ponto próximo (ou seja, , está no seu valor máximo utilizável - uma vez que geralmente se considera igual a 25cm (este valor também foi usado para fazer o gráfico acima).
- A ampliação linear é dada por . Assim que definimos (ver parte (b)), então isso mostra a igualdade nas ampliações.