Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.2 - Ex. 17

  1. Mostre que os valores de α para os quais a intensidade da figura de difração de uma fenda é máxima podem ser determinados exatamente derivando a Eq. 36-5 em relação a α e igualando o resultado a zero, o que leva à equação tan ⁡ α = α . Para determinar os valores de α que satisfazem essa equação, plote a curva y = tan ⁡ α e a linha reta y = α e determine as intersecções entre a reta e a curva ou use uma calculadora para encontrar por tentativas os valores corretos de α . A partir da relação α = m + 1 2 ⋅ π , determine os valores de m correspondentes a máximos sucessivos da figura de difração de fenda única. (Esses valores de m não são números inteiros porque os máximos secundários não ficam exatamente a meio caminho entre os mínimos.) Determine (b) o menor valor de α e (c) o valor de m correspondente, (d) o segundo menor valor de α e (e) o valor de m correspondente, (f) o terceiro menor valor de α e (g) o valor de m correspondente,

Passo 1

Para resolvermos esse exercício, vamos derivar a Eq. 36-5 e após isso plotar a curva que encontrarmos após a derivada. Vamos também manipular a expressão obtida para encontrarmos os valores de α para cada caso pedido.

Passo 2

Primeiramente, vamos chorar um pouco pelo tamanho do enunciado e as coisas bagunçadas que ele nos dá para descobrir o que é pra fazer. Pronto, vamos lá agora!

Para resolver o primeiro item, vamos começar derivando a Eq. 36-5 que é dada por

I = I m ⋅ sin 2 ⁡ α α 2

Se derivarmos essa equação em relação a α , vamos ter

d I d α = d d t I m ⋅ sin 2 ⁡ α ⋅ α - 2

Usando a regra do produto, vamos chegar que

d I d α = 2 ⋅ I m ⋅ sin 2 ⁡ α ⋅ cos ⁡ α ⋅ α - 2 - 2 ⋅ I m ⋅ sin 2 ⁡ α ⋅ α - 3 = 2 ⋅ I m ⋅ sin ⁡ α α 3 ⋅ α ⋅ cos ⁡ α - sin ⁡ α

Igualando toda essa equação a zero, chegamos que

2 ⋅ I m ⋅ sin ⁡ α α 3 ⋅ α ⋅ cos ⁡ α - sin ⁡ α = 0

Uma das soluções possíveis é que sin ⁡ α = 0 e α ≠ 0 . Logo, α = n ⋅ π , com n sendo um número inteiro. Se manipularmos um pouco mais a relação, podemos encontrar outro valor que também seja válido. Se observarmos a outra parte da equação, vemos que a igualdade também será válida caso

α ⋅ cos ⁡ α - sin ⁡ α = 0

tan ⁡ α = α

Se plotarmos y = tan ⁡ α e y = α , vamos ter que

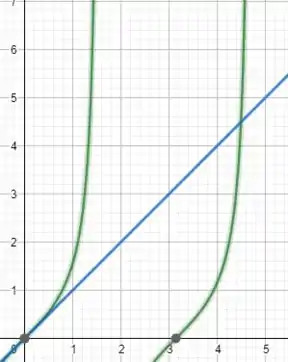
E os dois pontos de intersecção são os pontos em que a condição é respeitada.

Passo 3

Como vimos no gráfico da questão anterior, o menor valor possível de α é α = 0

Passo 4

Utilizando a Eq. Dada no enunciando, temos que α = m + 1 2 ⋅ π . Substituindo o menor valor de α , temos que

m + 1 2 ⋅ π = 0 → m = - 1 2

Passo 5

Utilizando um software para encontrar os outros pontos em que se satisfaz a relação, chegamos que o segundo mínimo é α = 4,493   r a d

Passo 6

Utilizando a Eq. Dada no enunciando, temos que α = m + 1 2 ⋅ π . Substituindo o menor valor de α , temos que

m + 1 2 ⋅ π = 4,493 → m = 0,930

Passo 7

Da mesma forma que anteriormente, chegamos que o terceiro mínimo é α = 7,725   r a d

Passo 8

m + 1 2 ⋅ π = 7,725 → m = 1,96

Resposta

b) α = 0   r a d

c) m = - 1 2

d) α = 4,493   r a d

e) m = 0,930

f) α = 7,725 r a d

g) m = 1,96

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando multiplicamos por dois a largura de uma fenda, a energia que passa pela fenda é multiplicada por dois, mas a intensidade do máximo central da figura é multiplicado por quatro. Explique quantita
Quando uma luz monocromática incide em uma fenda com 22,0μ m de largura, o primeiro mínimo de difração é obsevado para um ângulo de 1,80 ° em relação à direção da luz incidente. Qual é o comprimento d
Em um experimento de difração de fenda única, qual deve ser a razão entre a largura da fenda e o comprimento de onda para que o segundo mínimo de difração seja observado para um ângulo de 37,0 ° em re
Um experimento de difração de fenda única utiliza uma luz com um comprimento de onda de 420n m , que incide perpendiculamente em uma fenda com 5,10μ m de largura. A tela de observação está a 3,20m de
Qual deve ser a razão entre a largura da fenda e o comprimento de onda para que o primeiro mínimo de difração de uma fenda isolada seja observado para θ = 45,0 ° .