Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 73
O motorista de um carro deseja ultrapassar um caminhão que se desloca com velocidade constante de 20,0 m/s (aproximadamente 45 min/h). Inicialmente, o carro também se desloca com velocidade de 20,0 m/s e seu pára-choque dianteiro está 24,0 m atrás do pára-choque traseiro do caminhão. O motorista acelera com taxa constante de , a seguir volta para a pista do caminhão, quando a traseira de seu carro está a 26,0 m da frente do
caminhão. Ele possui comprimento de 4,5 m e o comprimento do caminhão é igual a 21,0 m. a) Qual o tempo necessário para o carro ultrapassar o caminhão? b) Qual a distância percorrida
pelo carro nesse intervalo de tempo? c) Qual é a velocidade final do carro?
Passo 1
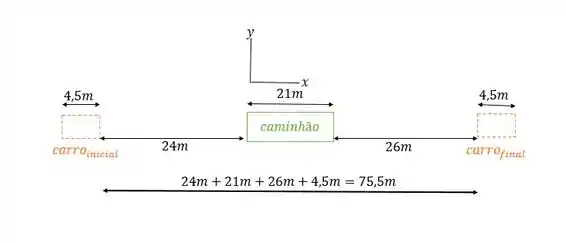
Vamos imaginar a situação, analisa-la e esboça-la:
É mais tranquilo pra gente, se colocarmos as coordenas referente ao caminhão. Observe que essas coordenadas se movem a uma velocidade constante em relação à Terra. Nestas coordenadas o caminhão está no referencial em repouso, e a velocidade inicial do carro é:
Além disso, a aceleração do carro nessas coordenadas é a mesma que em coordenadas fixadas na terra.
Passo 2
- Primeiro, vamos calcular a distância que o carro deve percorrer em relação ao caminhão:
- Agora vamos tomar como origem o ponto inicial do carro.
- E vamos calcular a velocidade final do carro por:
O carro vai de:
Para calcularmos o tempo que o carro leva para percorrer essa distancia, temos que:
Então podemos utilizar a seguinte equação:
O carro leva para passar o caminhão.
Passo 3
Assim, temos:
E vamos precisar, novamente da seguinte equação: