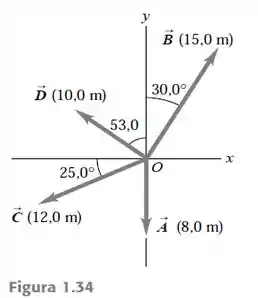
Para os vetores e indicados na Figura 1.34, a) ache o módulo e a direção do produto vetorial ; b) ache o módulo e a direção do produto vetorial .
Passo 1
- Precisamos analisar o ângulo entre e .
- Pelas propriedades do produto vetorial, sabemos que:
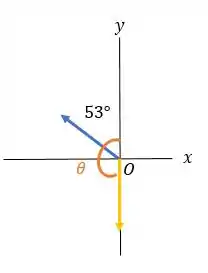
Passo 2
Sabemos que:
Assim,
Passo 3
- , o produto vetorial não é comutativo.
Ou seja, os resultado são os mesmo e direção também, porém o sentido que o vetor possui tem o sentido oposto ao outro.
Mas e a direção?
A direção dos vetores é a mesma. Os dois vetores passam pelo centro do eixo , perpendicular ao plano, pois os vetores precisam ser perpendiculares tanto à quanto a .
Ou seja, os resultado são os mesmo e direção também, porém o sentido que o vetor possui tem o sentido oposto ao outro.
Se você fizer a regra da mão direita, var ver que o produto escalar de estará em e o será no sentido , que vai estar “furando” a tela do seu PC.