Muita da pesquisa inicial sobre o movimento de foguetes foi feita por Robert Goddard, um professor de física no Clark College em Worcester, Massachusetts (EUA). Uma citação de um editorial de 1920 do New York Times ilustra a opinião pública sobre o seu trabalho: “Esse professor Goddard, com sua cátedra em Clark College e com o beneplácito da Smithsonian Institution, não conhece a relação entre ação e reação, e a nacessidade de algo melhor do que o vácuo contra o que reagir – notem o absurdo. Claramente ele apenas demonstra uma falta do conhecimento ministrado diariamente nos colégios.” A crença de que um foguete precisa de algo para empurrá-lo era um falso conceito comum, antes de os foguetes no espaço se tornarem habituais. Explique por que esta crença está errada.

Vamos desenhar o nossos projeto de foguete:

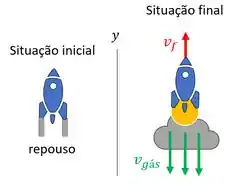
Se a gente considerar que não há agente externo, ou seja, forças externas, a quantidade de movimento do sistema formado pelo foguete e pelo combustível dentro dele deve se conservar. Ou seja:

Inicialmente, antes de lançar, o foguete está em repouso, Só que no repouso, a quantidade de movimento é nula .

A quantidade de movimento é dada por . Se na situação final o foguete adquiriu velocidade e o combustível dentro dele foi queimado e esse gás foi jogado para fora do foguete adquirindo velocidade , a quantidade total de movimento é

Então a conservação fica:

Como as massas são sempre positivas, essa expressão nos diz que a velocidade do foguete vai ter sentido oposto a velocidade do escape de gás do combustível.

E o que isso nos diz?

O que a conservação de quantidade de movimento nos diz é que quando o foguete queima combustível e o “empurra” para fora, esse combustível ganha velocidade para baixo, por isso o foguete ganha velocidade no sentido oposto, para cima e isso já é suficiente para impulsioná-lo.

Assim como alguém que fica de pé sobre uma prancha na água é empurrado para trás quando joga uma bola para frente.