Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 3- Ed: 6º - Capítulo 39.1 - Ex. 22

Uma nave espacial, em repouso em um determinado referencial S, recebe um aumento de velocidade de 0,50c (chame esse aumento de boost 1). Em relação ao seu novo quadro de repouso, a nave recebe um aumento adicional de 0,50c 10 segundos depois (conforme medido em seu novo quadro de repouso; chame este aumento de impulso 2). Esse processo é continuado indefinidamente, em intervalos de 10 s, conforme medido no quadro de repouso da nave. (Suponha que os impulsos levem um tempo muito curto em comparação com 10 s.) (A) Usando um programa de planilha, calcule e represente graficamente a velocidade da nave espacial no referencial S como uma função do número do impulso para o impulso 1 ao impulso 10. (b) Represente graficamente o fator gama da mesma maneira. (c) Quantos impulsos são necessários até que a velocidade do navio em S seja maior que 0,999c? (d) A que distância a nave se move entre o impulso 1 e o impulso 6, medido no referencial S? Qual é a velocidade média da espaçonave entre o impulso 1 e o impulso 6, medida em S?

Passo 1

Fala aee, beleza??

Vamos deixar a velocidade (em S ) da espaçonave após o i-ésimo impulso ser v i e achar uma expressão para a razão de v para c após o ( i + 1 )º impulso da nave espacial como uma função do número de impulsos N .

Além disso, podemos usar a definição de γ , em termos de v / c para representar graficamente γ como uma função de N . Vamos lá!

Passo 2

Então, vamos fazer a (a) e a (b) ao mesmo tempo rs. A velocidade da nave após o ( i + 1 )º impulso será dado por:

v i + 1 = v i + 0,5 c 1 + 0,5 c v i c 2

v i + 1 = v i + 0,5 c 1 + 0,5 v i c

Assim, v i + 1 c :

v i + 1 c = v i c + 0,5 1 + 0,5 v i c

E também temos que:

γ i = 1 1 - v i 2 c 2

Passo 3

Então, vamos construir uma tabela com os valores de N , v / c e γ :

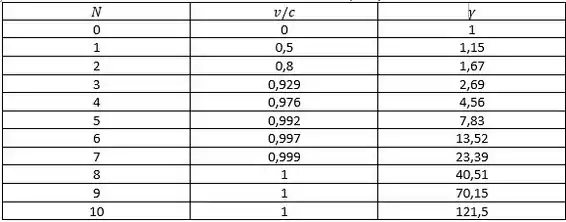
Assim, o gráfico de v / c em função de N fica:

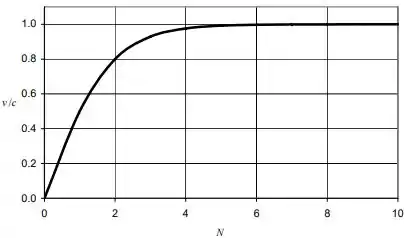
E o gráfico de γ em função de N :

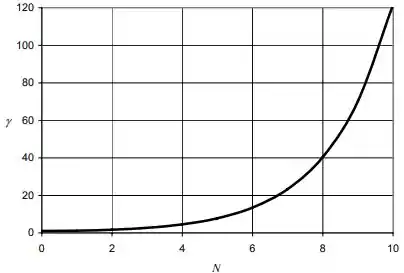
Passo 4

(c) Bem, olhando a tabela ou o gráfico de v / c em função de N vemos que, após 8 impulsos, a velocidade da nave já é maior que 0,999 c .

Passo 5

(d) A velocidade média da espaçonave, entre o impulso 1 e o impulso 5, medida em S é dada por:

v m é d = ∆ x ∆ t

Onde Δt é o tempo de viagem medido no referencial da Terra.

Passo 6

Após 5 impulsos, a espaçonave percorreu uma distância Δ x , medida no referencial da Terra (S), dada por:

∆ x = ∆ x 1 → 2 + ∆ x 2 → 3 + ∆ x 3 → 4 + ∆ x 4 → 5 + ∆ x 5 → 6

∆ x = 0,5 c 10 s γ 1 → 2 + ( 0,8 c ) ( 10 s ) γ 2 → 3 + ( 0,929 c ) ( 10 s ) γ 3 → 4 + 0,976 c ( 10 s ) γ 4 → 5 + ( 0,992 c ) ( 10 s ) γ 5 → 6

∆ x = 0,5 c 10 s ( 1,15 ) + ( 0,8 c ) ( 10 s ) ( 1,67 ) + ( 0,929 c ) ( 10 s ) ( 2,69 ) + 0,976 c ( 10 s ) ( 4,56 ) + ( 0,992 c ) ( 10 s ) ( 7,83 )

∴

∆ x = 166   c ∙ s

Só falta expressar Δ t como a soma das vezes que a espaçonave viaja durante cada intervalo de 10 s após um aumento em sua velocidade:

∆ t = ∆ t 1 → 2 + ∆ t 2 → 3 + ∆ t 3 → 4 + ∆ t 4 → 5 + ∆ t 5 → 6

∆ t = 10 s γ 1 → 2 + 10 s γ 2 → 3 + 10 s γ 3 → 4 + ( 10 s ) γ 4 → 5 + ( 10 s ) γ 5 → 6

∆ t = 10 s ( 1,15 ) + ( 10 s ) ( 1,67 ) + ( 10 s ) ( 2,69 ) + ( 10 s ) ( 4,56 ) + ( 10 s ) ( 7,83 )

∴

∆ t = 1 79   s

Passo 7

Agora, é só substituir esses valores na velocidade média:

v m é d = 166   c ∙ s 179   s

v m é d = 0,927 c

Pronto!! Acabou!

Resposta

(a)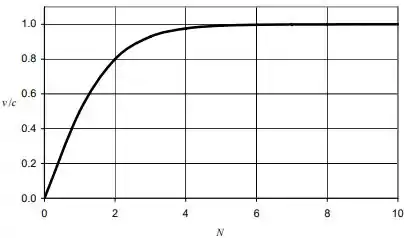

(b)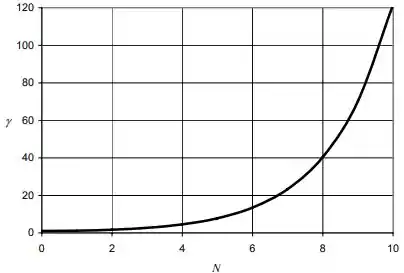

(c) após 8 impulsos

(d) 0,927 c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59 . A espaçonave I, que transporta estudantes realizando um exame de Física, se aproxima da Terra a uma velocidade de 0,600 c (em relação à Terra), enquanto a espaçonave II, transportando professores
63 . Owen e Dina estão em repouso no referencial S ’ , que se move a 0,600 c em relação a S . Eles brincam de jogar bola um para o outro enquanto Ed, em repouso no referencial S , assiste à ação (Fig.
A transformação de Lorentz para y e z é igual ao resultado clássico: y = y ′ e z = z ′. No entanto, a transformação relativística da velocidade não dá o resultado clássico uy = u 'y e z z u = u'. Expl
Uma nave espacial está se movendo para o leste a uma velocidade de 0,90c em relação à Terra. Uma segunda espaçonave está se movendo para oeste à velocidade de 0,90c em relação à Terra. Qual é a veloci