Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 9.Problemas - Ex. 63
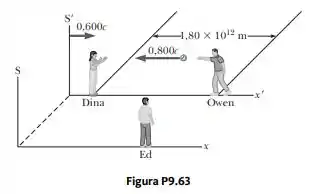
Owen e Dina estão em repouso no referencial , que se move a em relação a . Eles brincam de jogar bola um para o outro enquanto Ed, em repouso no referencial , assiste à ação (Fig. P9.63). Owen arremessa a bola para Dina a (segundo Owen) e a separação (medida em ) é igual a . Segundo Dina, a bola se move a que velocidade? Segundo Dina, qual é o intervalo de tempo necessário para que a bola a alcance? Segundo Ed, qual a distância entre Owen e Dina, com que velocidade a bola se move e qual intervalo de tempo é necessário para que a bola alcance Dina?
Passo 1
Para resolver bem esse exercício temos que ter na cabeça duas coisas fundamentais:
Como descobrir o tempo através de:
A contração de Lorentz:
Onde é o comprimento próprio.
E a soma das velocidades relativísticas:
Só isso? Só isso!
Bora lá então...
Passo 2
Como Dina está junto de Owen no referencial em movimento então para ela a bola se move com a mesma velocidade que Owen arremessou, ou seja, .
Passo 3
Para descobrir esse tempo vamos usar e substituir os valores que o enunciado nos dar.
Passo 4
O comprimento próprio é aquele medido no referencial no qual o que está sendo medido está estacionário, ou seja, como o que está sendo medido é a distância entre Dina e Owen então o comprimento próprio será .
Como queremos a distância entre eles segundo Ed temos que:
Passo 5
Agora vamos usar a soma das velocidades relativísticas com os valores que conhecemos e obter a velocidade que ver a bola.
Bora bora que só falta uma!!
Passo 6
Para responder esse item vamos usar o valor de que achamos no Passo 4 pois enquanto a Dina se move para direita a bola se move para esquerda (uma indo ao encontro da outra) e a soma das velocidade que foi encontrada no Passo 5, ou seja:
Resposta