Exercícios de Transformada de Lorentz para a Velocidade - Lista de Exercícios Resolvida

Uma partícula está se movendo ao longo do eixo do referencial com uma velocidade . O referencial está se movendo com uma velocidade de em relação ao referencial . Qual é a velocidade da partícula no referencial ?

Duas partículas são produzidas em um acelerador de partículas de alta energia e se afastam em sentidos opostos.

A velocidade de uma das partículas, medida no laboratório, é igual a , e a velocidade relativa entre as duas é de .

Qual é o módulo da velocidade da outra partícula, medida no laboratório?

Uma nave do planeta Tatooine está tentando alcançar um cruzador da Federação do Comércio. Em relação a um observador em Tatooine, o cruzador está se afastando do planeta com uma velocidade de .

A nave está se deslocando com uma velocidade de em relação a Tatooine, no mesmo sentido que o cruzador.

1. Para a nave alcançar o cruzador, a velocidade do cruzador em relação a ela deve ser positiva ou negativa?
2. Qual é a velocidade do cruzador em relação à nave?

Uma espaçonave da Armada Imperial se desloca com velocidade elevada em relação ao planeta Arrakis e dispara um foguete na direção do planeta com uma velocidade de em relação à espaçonave.

Um observador na superfície da Arrakis verifica que o foguete está se aproximando com velocidade de .

Qual é a velocidade da espaçonave em relação ao planeta Arrakis?

A espaçonave está se aproximando ou se afastando de Arrakis?

Em algum momento no futuro da Terra…

Descobre-se que um asteroide, a 120 milhões de quilômetros de distância, tem sua trajetória em rota de colisão com a Terra. A velocidade do asteroide é não-relativística e para todos os efeitos práticos pode ser desprezada. A agência espacial americana manda, em t =0, uma nave não tripulada em direção ao asteroide, com velocidade (medida na Terra). Considere o sistema de referência da nave () tendo e (origem de posição e tempo coincidentes para a Terra e a nave), sendo a direção definida entre a Terra e o asteroide.

No mesmo momento em que a nave é lançada, a agência espacial brasileira manda um míssil em direção ao asteroide. O míssil explode no asteroide 8min20s após o lançamento, de acordo a relógios na Terra.

(b) Qual é a velocidade do míssil, medida pela nave? Em que instante de tempo, de acordo ao computador de bordo da nave, o míssil explode no asteroide?

A nave 1 (referencial ) viaja com uma velocidade constante de no sentido , afastando-se da Terra (referencial ). Dentro da nave 1 há um relógio atômico que foi sincronizado com outro na Terra no mento em que a nave passou pela Terra.

a) O relógio atômico, de Cs-133, se caracteriza por ter oscilações por segundo em seu referencial de repouso. Visto por um observador na Terra, qual é o número de oscilações por segundo do relógio atômico que se encontra na nave 1?

b) Medidas feitas por relógios terrestres mostram que dois relâmpagos caíram simultaneamente nas cidades de Quito (equador) e Pekanbaru (Indonésia). Essas cidades estão diametralmente opostas sobre a linha do Equador. Encontre as separações espacial () e temporal () entre esses dois eventos vistos por um observador na nave 1.

Dado: o raio equatorial da Terra é de .

c) Uma outra nave, nave 2, também se movimentando sobre o eixo , vê o relâmpago caindo em Quito após aquele caindo em Pekanbaru. Compare essa observação com o resultado da letra (b) e argumente o que pode ser concluído sobre o movimento da nave 2 em relação à Terra.

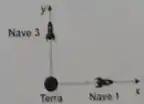
d) Uma terceira nave, Nave 3, se move com velocidade , medida pela Terra, em uma direção perpendicular à nave 1, como mostrado na figura. Qual o módulo da velocidade da nave 3 medida pela nave 1?

Uma nave se afasta de uma estação (referencial inercial) com velocidade (em relação à estação) lança um foguete com velocidade (em relação à nave). Para um observador na estação, a velocidade do foguete em módulo vale

a) .

b) .

c) .

d) .

Dois foguetes disputam a final de um torneio intergaláctico de velocidade. Para o referencial inercial S, o cronômetro é zerado no momento da largada, o foguete A parte da posição e , com velocidade constante de , o foguete B parte da posição e , com velocidade constante de e o foguete ganhador e aquele que primeiro passar pela linha de chegada, posicionada em . Despreze os tamanhos dos foguetes. Essa mesma corrida pode ser vista de um referencial inercial preso ao foguete A, denominado , ou de um referencial inercial preso ao foguete B, denominado , os quais dividem a origem de seus eixos coordenados com o referencial S no instante da largada.

Em função dos dados do enunciado e de constantes fundamentais dadas no formulário (folha de capa), calcule e responda o que se pede.

(C) Do ponto de vista do referencial inercial , determine.

i) As velocidades dos foguetes A e B.

ii) O intervalo de tempo entre a largada e o momento em que o foguete A cruza a linha de chegada.

iii) O intervalo de tempo entre a largada e o momento em que o foguete B cruza a linha de chegada.

iv) Qual foguete é campeão do torneio de arrancada intergaláctica?

Dadas as transformações de coordenadas de Lorentz entre dois referenciais

inerciais, obtenha a expressão para a transformação de velocidades de Lorentz. Admita

uma partícula com velocidade u no referencial S. Obtenha a velocidade u ́ da partícula

no referencial S ́. Admita o referencial S ́ se movendo com velocidade v em relação a S.

Uma esquadrilha de espaçonaves com 1,00 anos-luz de comprimento (no seu referencial de repouso) está se movendo com velocidade 0,80c em relação a uma base espacial. Uma nave mensageira viaja da retaguarda da esquadrilha com velocidade 0,95c em relação à base espacial.

(a ) Calcule quanto tempo leva a viagem da nave mensageira em seu próprio referencial.

(b ) Obtenha o intervalo de tempo gasto pela nave mensageira no referencial da esquadrilha.

(c ) Determine quanto tempo leva a viagem da nave mensageira em relação à base espacial.

Dois foguetes disputam a final de um torneio intergaláctico de velocidade. Para o referencial inercial S, o cronômetro é zerado no momento da largada, o foguete A parte da posição e , com velocidade constante de , o foguete B parte da posição e , com velocidade constante de e o foguete ganhador e aquele que primeiro passar pela linha de chegada, posicionada em . Despreze os tamanhos dos foguetes. Essa mesma corrida pode ser vista de um referencial inercial preso ao foguete A, denominado , ou de um referencial inercial preso ao foguete B, denominado , os quais dividem a origem de seus eixos coordenados com o referencial S no instante da largada.

Em função dos dados do enunciado e de constantes fundamentais dadas no formulário (folha de capa), calcule e responda o que se pede.

(B) Do ponto de vista do referencial inercial , determine.

i) As velocidades dos foguetes A e B.

ii) O intervalo de tempo entre a largada e o momento em que o foguete A cruza a linha de chegada.

iii) O intervalo de tempo entre a largada e o momento em que o foguete B cruza a linha de chegada.

iv) Qual foguete é campeão do torneio de arrancada intergaláctica?

Um feixe de luz monocromático se propaga ao longo do eixo de um referencial inercial com velocidade . Um referencial inercial se move com velocidade , em relação ao referencial . O vetor velocidade do feixe de luz para o referencial é dado por:

a) .

b) .

c) .

d) .

e) .

Em uma perseguição intergaláctica, ladrões tentam escapar em um foguete que possui velocidade de enquanto outra nave tripulada por soldados possui velocidade . Determine a velocidade do foguete em relação à nave.

a) .

b) .

c) .

d) .

e) .

Considere dois referenciais inerciais e , com origens e , respectivamente. O referencial move-se com velocidade em relação a .

a) Se um foguete é lançado de com velocidade , qual é a velocidade de lançamento do foguete para um observador em repouso em ?

b) Supondo agora que dois pulsos de luz sejam enviados simultaneamente em dos pontos e na direção de um detector colocado na origem . Obtenha os intervalos de tempo entre as detecções dos pulsos de luz em , medidos por observadores nos sistema e .

Um referencial inercial move-se com vetor velocidade em relação ao referencial inercial .

Sabemos que um projétil viaja numa trajetória retilínea no plano fazendo um ângulo com o eixo e que a componente do seu vetor velocidade é um quarto da velocidade da luz no vácuo.

1. Quais as componentes do vetor velocidade no referencial ?
2. Qual é o ângulo dessa trajetória em relação ao eixo ?
3. Qual seria esse ângulo no referencial se no lugar do projétil tivermos um fóton?

Uma espaçonave move-se em relação à Terra com uma velocidade constante de . A espaçonave tem uma forma aproximadamente cilíndrica, com de comprimento, em seu referencial próprio.

Dentro da espaçonave há um emissor de elétrons, situado na parte de trás da nave. Os elétrons são lançados com velocidade constante em relação à espaçonave, propagam-se no vácuo e atingem a parte da frente da espaçonave.

Para um observador na Terra, calcule:

1. O intervalo de tempo que os elétrons levam para ir de um extremo ao outro.
2. A distância que os elétrons percorrem.
3. A velocidade dos elétrons.
4. O comprimento da nave.

Um observador parado na Terra vê uma espaçonave passar com velocidade .

Na ponta da espaçonave, uma partícula é lançada para trás, com velocidade c, em relação à espaçonave.

Qual a velocidade da partícula para o observador na Terra?

10. Nenhuma das anteriores.

Uma nave espacial se afasta da Terra com velocidade em relação à Terra. Em , a nave lança um míssil, que viaja com velocidade em relação à nave, na mesma direção da mesma.

(a) Determine a velocidade do míssil em relação à Terra.

(b) Considerando que a nave espacial viaja em direção a uma localidade situada a uma distância D segundo observadores na Terra, determine o tempo necessário para que a nave atinja a localidade segundo seu comandante.

Em uma corrida intergaláctica, o foguete A é colocado na posição e o fogute B em para um dado referencial . O objetivo da corrida é chegar na posição primeiro. A largada é dada no instante para o referencial inercial e os foguetes saem nesse instante com velocidades e , respectivamente.

Em função dos dados do enunciado, calcule o que se pede.

a) Determine os instantes de tempo para os quais os foguetes A e B cruzam a linha de chegada para o referencial ;

b) Determine a velocidade do foguete A em relação a uma referencial inercial ligado ao foguete B.

c) Determine os instantes de largada e chegada de cada foguete em relação a um referencial inercial ligado ao foguete B.

Duas partículas possuem velocidades e em relação a um referencial inercial. O módulo da velocidade de uma delas com respeito à outra vale:

a) .

b) .

c) .

d) .

e) .

Duas naves espaciais, 1 e 2, movem-se em relação a um referencial inercial, ao longo do eixo , com as equações de movimento (posição versus tempo) e , respectivamente. A equação horária de movimento da nave , , para um referencial inercial preso à nave é dada por (considere como o tempo marcado pelo referencial preso à nave ):

a) .

b) .

c) .

d) .

e) .

f) .

Uma barra de comprimento próprio L, orientada segundo um ângulo em relação ao eixo

x está em repouso em um sistema inercial S, conforme a figura. Considere um sistema S’

que se move com velocidade constante em relação a S. Nos itens abaixo expresse

suas respostas em termos de L, , , e da velocidade da luz c.

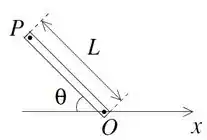
(c) Suponha agora que uma partícula relativística se move ao longo da barra com velocidade V , medida em S, no sentido de P para O. Quais são as componentes do vetor velocidade desta partícula para um observador em S’?