Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 1.Problemas - Ex. 89
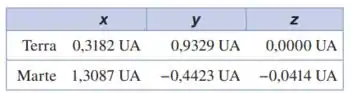
Navegando no sistema solar. A espaçonave Mars Polar Lander (explorador polar de Marte) foi lançada em 3 de janeiro de 1999. No dia 3 de dezembro de 1999, ela pousou na superfície de Marte em alta velocidade e provavelmente se desintegrou, ocasião em que as posições de Marte e da Terra eram dadas pelas seguintes coordenadas:
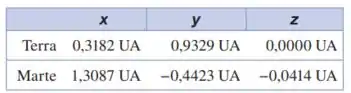
Nessas coordenadas, o Sol está na origem e o plano da órbita da Terra é o xy. A Terra corta o eixo +x uma vez por ano no equinócio do outono, o primeiro dia de outono no Hemisfério Norte, o que ocorre em torno do dia 22 de setembro. Uma UA, ou unidade astronômica, equivale a 1,496 × 108 km, a distância média entre a Terra e o Sol. (a) Em um diagrama, mostre as posições do Sol, da Terra e de Marte no dia 3 de dezembro de 1999. (b) Calcule as seguintes distâncias em UA no dia 3 de dezembro de 1999: (i) entre o Sol e a Terra; (ii) entre o Sol e Marte; (iii) entre a Terra e Marte. (c) Observando-se da Terra, qual era o ângulo entre a direção que unia a Terra a Marte e a direção que unia a Terra ao Sol no dia 3 de dezembro de 1999? (d) Verifique e explique se Marte era visível à meia-noite na sua cidade no dia 3 de dezembro de 1999. (Quando é meia-noite no seu local, o Sol está do lado oposto da Terra em relação a você.)
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha de vetores?
O enunciado dessa é bem grande, então vamos devagarzinho... A quest��o nos dá as coordenadas em unidades astronômicas da Terra e de Marte:
Lembrando que se o objeto A tem coordenadas e o objeto B tem coordenadas , o vetor de A até B tem o componente :
E o componente :
Passo 2
Letra a:
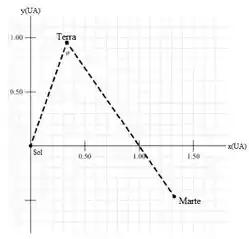
Queremos mostre as posições do Sol, da Terra e de Marte no dia 3 de dezembro de 1999 em um diagrama.
O diagrama é esboçado na figura:
Passo 3
Letra b:
Aqui queremos calcular as seguintes distâncias em UA no dia 3 de dezembro de 1999:
- entre o Sol e a Terra;
- entre o Sol e Marte;
- entre a Terra e Marte.
Em UA:
(i)
(ii)
(iii)
Passo 4
Letra c:
Aqui queremos encontrar o ângulo entre a direção que unia a Terra a Marte e a direção que unia a Terra ao Sol no dia 3 de dezembro de 1999.
O ângulo entre as direções da Terra ao Sol e a Marte é obtido a partir do produto.
Combinando as equações temos:
Passo 5
Letra d:
Bom... Marte não poderia ser visível à meia-noite, porque o ângulo Sol-Marte é menor que 90º.
Nossos cálculos dão corretamente que Marte está mais longe do Sol do que a Terra.
Observe que nesta data, Marte estava mais longe da terra do que do sol.
Resposta
- Ver diagrama
- Ver respostas
- Marte não poderia ser visível à meia-noite, porque o ângulo Sol-Marte é menor que 90º.