Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.Problemas - Ex. 78
A extremidade de uma mola horizontal com constante de força igual a é presa a um poste vertical. Um bloco de de gelo sem atrito é preso à outra extremidade e apoia-se no piso. A mola inicialmente não se encontra esticada nem comprimida. Uma força horizontal constante de é então aplicada ao bloco, no sentido contrário ao poste. (a) Qual é a velocidade do bloco quando a mola é esticada por ? (b) Nesse instante, quais são o módulo, a direção e o sentido da aceleração do bloco?
Passo 1
Fala galerinha, beleza?
Vamos desenhar primeiro as forças relevantes para o problema:
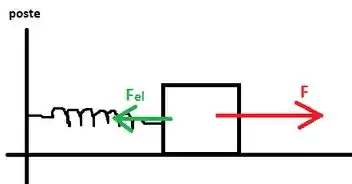
Não desenhei o peso e a normal pois o trabalho delas será nulo já que o deslocamento é horizontal. Como o corpo se desloca para a direita, temos que
A força elástica aponta para a esquerda pois a mola será esticada e força elástica é uma força do tipo restauradora.
O trabalho da força é fácil de calcular pois ela é constante:
Passo 2
Vamos calcular agora o trabalho da força elástica. Como essa força não é constante ao longo do movimento, vamos precisar fazer uma integral:
Sabemos que , onde é a deformação da mola, de modo que
Usando e , temos que
Com isso, podemos somar todos os trabalhos para achar o trabalho da força resultante:
Passo 3
Agora que temos o trabalho, basta usar o teorema trabalho-energia:
Como o bloco parte do repouso, temos que :
Portanto,
Passo 4
Para resolver o item (b) vamos calcular primeiro a força resultante. A força elástica (em módulo) é
Como a força ganha a disputa, a força resultante sobre o bloco aponta para a direita:
Para achar a aceleração, usamos