Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 75

Um objeto com secção transversal de área A é disparado horizontalmente sobre gelo desprovido de atrito. Sua velocidade inicial é v 0 x   no instante t 0 = 0   s . A resistência do ar não é desprezível.

  1. Mostre que a velocidade em um instante t é dada pela expressão

    2. v x = v 0 x 1 + A v 0 x t / 4 m

  2. Um carro de 1.500 kg, 1,6 m de largura e 1,4 m de altura se depara com um trecho congelado e muito liso quando está se deslocando a 20 m/s. Se o atrito for desprezível, quanto tempo levará para a velocidade do carro diminuir para 10 m/s? E para reduzir-se a 5 m/s?
  3. Avalie se, neste caso, é plausível ou não desprezar o atrito cinético.

Passo 1

Modelaremos o objeto como uma partícula e usaremos o modelo de arrasto.

Nós conhecemos   v 0 x , m a s s a = m , t 0 = 0 , á r e a   d e   s e ç ã o   t r a n s v e r s a l = A . E queremos encontra v x .

Passo 2

Vamos entender melhor a situação:

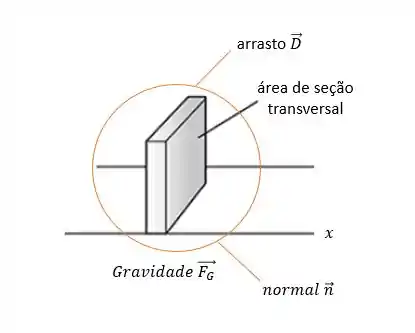
E desenhar um diagrama de corpo livre:

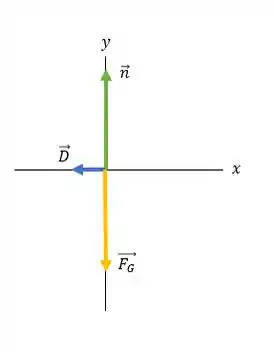
Passo 3

  1. Não podemos usar as equações cinemáticas de aceleração constante, pois a força de arrasto faz com que a aceleração mude com o tempo. Em vez disso, devemos usar a x = d v x / d t e integrar para encontrar v x . A segunda lei de Newton para o objeto é

    2. F t o t a l x = ∑ F x = n x + P x + f k x + D x = 0 N + 0 N + 0 N - 1 4 A v x 2 = m a x = m d v x d t

    Isso pode ser escrito:

    d v x v x 2 = A 4 m d t

    Podemos integrar isso desde o início ( v 0 x em t = 0 ) até o fim ( v x   em t ):

    ∫ v 0 x v x d v x v x 2 = A 4 m ∫ 0 t d t ⇒ - 1 v x + 1 v 0 x = A 4 m t

    Resolvendo para v x , nós temos que:

    v x = v 0 x 1 + A v 0 x t / 4 m

    Passo 4

  2. Usando A = 1,6 m 1,4 m = 2,24 m 2 , v 0 x = 20   m / s e m = 1500   k g , nós temos que:

    3. v x = 20 m s 1 + 2,24 t 20 4 × 1500 = 20 1 + 0,007467

    ⇒ t = 1 0,007467 20 m s v x - 1

    onde t é em segundos. Agora podemos obter o tempo t para v   =   10   m   /   s :

    t = 1 0,007467 20 m s 10 m s - 1 = 133,93 20 10 - 1 = 134 s

    Quando v x = 5   m / s , então t   =   402   s .

    Passo 5

  3. Se a única força que age sobre o objeto foi o atrito cinético com, digamos, μ k = 0,05 , essa força seria ( 0,05 )   ( 1500   k g )   ( 9,8   m / s 2 ) = 735   N . A força de arrasto a uma velocidade média de 10   m / s é D = 1 4 2,24 10   N 2 = 56   N . Concluímos que não é razoável negligenciar a cinética da força de fricção.

Resposta

  1. Mostrado no passo 2
  2. Quando v x = 10   m / s , então t   =   134   s .

    3. Quando v x = 5   m / s , então t   =   402   s .

  3. Não é plausível
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a Eq. 6-14 forneça a força de arrasto a que estão sujeitos um piloto e o assento de ejeção imediatamente após terem sido ejetados de um avião voando horizontalmente a 1300k m / h . Suponha
Calcule a razão entre a força de arrasto experimentada por um avião a jato voando a 1000k m / h a uma altitude de 10k m e a força de arrasto experimentada por um avião a hélice voando a metade d
Ao descer uma encosta, um esquiador é freado pela força de arrasto que o ar exerce sobre o seu corpo e pela força de atrito cinético que a neve exerce sobre os esquis. (a) Suponha que o ângulo da enco
Continuação do Problema 8. Suponha agora que a Eq. 6-14 forneça o módulo da força de arrasto que age sobre uma pedra típica de 20k g , que apresenta ao vento uma área de seção reta vertical de 0,040m
Continuação dos Problemas 8 e 37. Outra explicação é que as pedras se movem apenas quando a água que cai na região durante uma tempestade congela, formando uma fina camada de gelo. As pedras ficam pre