Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.4 - Ex. 38
Ao descer uma encosta, um esquiador é freado pela força de arrasto que o ar exerce sobre o seu corpo e pela força de atrito cinético que a neve exerce sobre os esquis. (a) Suponha que o ângulo da encosta é , que a neve é seca, com um coeficiente de atrito cinético , que a massa do esquiador e seu equipamento é , que a área da seção reta do esquiador (agachado) é , que o coeficiente de arrasto é e que a massa específica do ar é . (a) Qual é a velocidade terminal? (b) Se o esquiador pode fazer o coeficiente de arrasto sofrer uma pequena variação alterando, por exemplo, a posição das mãos, qual é a variação correspondente da velocidade terminal?
Passo 1
Show de bolinhas pessoal, podemos começar esse exercício fazendo o DCL do esquiador:
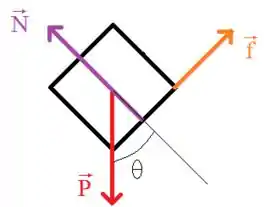
Lembrando que como o esquiador está em movimento, então devemos usar a força de atrito cinético, que pode ser calculada a partir da seguinte relação:
A partir da ilustração, podemos aplicar a segunda lei de Newton no eixo para determinar a força de arrasto:
Como no eixo não há movimento e, portanto, está em equilíbrio, podemos determinar a normal em fução da componente do peso:
Por fim, devemos lembrar da equação da velocidade terminal:
Passo 2
Na vamos substituir a já com o valor da normal dado na :
Substituindo os valores dados no enunciado:
Passo 3
Com a força de arrasto determinada, podemos substituir na :
Passo 4
Quando o exercício fala de pequenas variações ele nos remete a derivada. Assim, devemos derivar a em função de . Assim:
Isolando e substituindo os valores conhecidos:
Resposta
- ;
- .