Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 8b

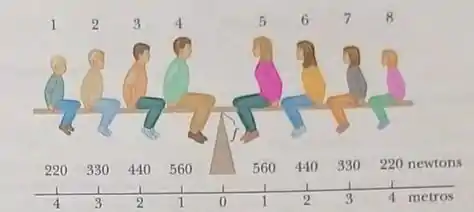
Oito alunos de física, cujos pesos estão indicados em newtons na Figura, se equilibram em uma gangorra. Qual é o número do estudante que produz o maior torque em relação a um eixo de rotação que passa pelo fulcro no sentido (a)para fora do papel e (b)para dentro do papel?

Passo 1

(b)Primeiro, precisamos lembrar aqui da definição de torque, geralmente representado pela letra .

Ele é igual ao produto entre uma força e o seu “braço”, que é a distância entre sua linha de atuação e o ponto em relação ao qual a gente calcula esse torque. Esse mesmo produto é representado pelo produto vetorial: .

A direção do vetor resultante desse produto é obtida pela regra da mão direita, como no caso abaixo:

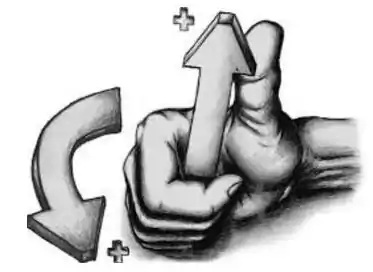
Nesse caso, como , temos que colocar os 4 dedos na direção de (que vai no sentido do eixo para o ponto de aplicação da força) e fechar a mão na direção de . estará na direção do nosso polegar.

Passo 2

Com base na regra da mão direita, a gente já consegue observar que os torques que estão no sentido para fora do papel (com relação ao ponto ) são exercidos pelos alunos que estão à esquerda (alunos ), lembrando que as forças que eles exercem sobre a gangorra estão direcionadas para baixo. Para identificar o aluno que dentre esses exerce o maior torque, temos que comparar os produtos entre seus pesos e a distâncias que eles estão de .