Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.1 - Ex. 8
Ondas sonoras com uma frequência de 3000 Hz e uma velocidade de 343 m/s passam pela abertura retangular de uma caixa de som e se espalham por um grande auditório de comprimento . A abertura, que tem uma largura horizontal de 30,0 cm, está voltada para uma parede que fica a 100 m de distância (Fig, 36-36). Ao longo dessa parede, a que distância do eixo central está o primeiro mínimo de difração, posição na qual um espectador terá dificuldade para o ouvir o som? (Ignora as reflexões.)
Passo 1
Nesse exercício vamos utilizar a equação para o mínimo de difração e as relações trigonométricas para estabelecer conexões entre a distância em que ouvinte terá dificuldades para ouvir e a expressão para o mínimo da difração
Passo 2
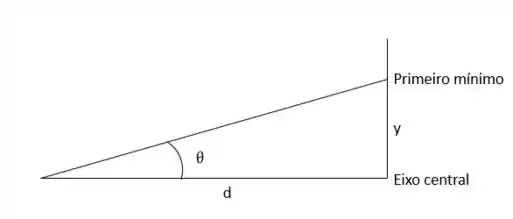
Analisando a belíssima imagem acima, podemos ver que é possível estabelecer uma relação para encontrarmos o , que é a distância onde o ouvinte terá dificuldades para ouvir. Assim, podemos escrever da seguinte forma
Temos também que a relação do mínimo é dada por . Substituindo nosso valor de seno na equação, chegamos que
Elevando toda a equação ao quadrado, temos que
Substituindo os valores que temos, assumindo para o primeiro mínimo de difração e substituindo o comprimento de onda pela frequência através da relação , temos que
Logo, é a distância onde um ouvinte começara a ter dificuldades para ouvir o som emitido.
Resposta
.