Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 114
Passo 1
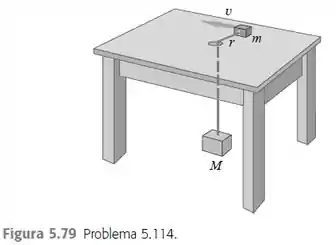
Eaee, belezinha?? Bom... o enunciado nos diz que um pequeno bloco de massa repousa sobre o topo de uma mesa horizontal sem atrito a uma distância de um buraco situado no centro da mesa.
Um fio ligado ao bloco pequeno passa através do buraco e tem um bloco maior de massa ligado em sua outra extremidade.
O pequeno bloco descreve um movimento circular uniforme com raio e velocidade .
Queremos calcular o valor de para que o bloco grande permaneça imóvel quando libertado.
Bom... O grande lance aqui é perceber que o movimento circular do bloco menor que vai manter o bloco maior suspenso através da tensão da corda entre eles.
Também devemos saber que a força centrípeta é dada por:
Onde é a velocidade e é o raio.
Passo 2
A tensão na corda deve ser o mesmo valor que o peso do bloco suspenso e, ao mesmo tempo, fornecer a força necessária para manter o bloco em movimento circular uniforme.
Ou seja,
Agora que entendemos o sistema, vamos atrás da velocidade!
Passo 3
Vamos trabalhar com a igualdade:
Agora basta isolar o valor de :