Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 115
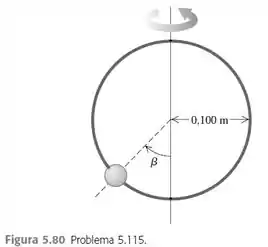
Uma pequena conta pode deslizar sem atrito ao longo de um aro circular situado em um plano vertical com raio igual a . O aro gira com uma taxa constante de em torno de um diâmetro vertical (Figura 5.80).
a) Ache o ângulo para o qual a conta está em equilíbrio vertical. (É claro que ela possui uma aceleração radial orientada para o eixo da rotação.)
b) Verifique se é possível a conta “subir” até uma altura igual ao centro do aro.
c) O que ocorreria se o aro girasse com ?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma pequena conta pode deslizar sem atrito ao longo de um aro circular situado em um plano vertical com raio igual a .
O aro gira com uma taxa constante de em torno de um diâmetro vertical de acordo com a seguinte figura:
Queremos encontrar o ângulo para o qual a conta está em equilíbrio vertical e verificar se é possível a conta “subir” até uma altura igual ao centro do aro.
Também deveremos analisar o que ocorreria se o aro girasse com .
Para resolver tudo isso, precisaremos decompor as forças na vertical e na horizontal.
Também devemos saber que a força centrípeta é dada por:
Onde é a velocidade e é o raio.
Passo 2
- Antes de tudo temos que ver que tem dois movimentos aí: a conta (você pode imaginar que é uma missanga) em volta do aro e o aro em torno dele mesmo.
- Para subir até o centro do aro, o ângulo deve ser , e . Achamos essa relação do cosseno desse ângulo com o período, saca só:
- Agora temos uma nova frequência, e assim um novo período. Vamos calcular o novo período primeiro:
Sobre essa conta está agindo o peso, vertical para baixo, e a normal, que é radial e aponta para o centro da trajetória.
A componente vertical da normal deve contrabalançar a forma peso, enquanto que a componente horizontal deve ser igual a força resultante radial.
Além disso, temos que a força normal será dependente do ângulo .
Vamos equacionar as forças.
Na vertical:
Na horizontal:
Passo 3
E, igualando essas duas relações (verticais e horizontais), teremos apenas como variável o ângulo :
Ajeitando,
Onde é a aceleração radial e é a aceleração da gravidade.
Pronto! Achamos a relação de , agora vamos desenvolver um pouco mais!
Passo 4
Como temos um movimento circular temos que a aceleração radial será,
mas não temos a velocidade no ponto. Então vamos reescrever a velocidade em termos do período de revolução:
E assim a aceleração radial também pode ser reescrita:
Temos que , então a aceleração radial fica:
E substituindo na relação encontrada do Passo 1:
Passo 5
Agora sim! Ufa! Podemos simplificar o seno e reescrever, olha só:
Ajeitando,
O enunciado forneceu a frequência,
então o período fica
Como o raio é , . Agora é só substituir:
Passo 6
Daí, se tivermos o cosseno indo a zero, isso significa que o período também vai a zero. E sabemos que quanto menor o período, maior a velocidade.
Resumindo, se , e por consequência .
A conta deveria girar muuuuuito rápido para conseguir subir. Então isso não é possível, ok?
Passo 7
Ok, agora vamos calcular o novo valor do cosseno do ângulo:
Xii, não existe nenhum valor de que satisfaça essa solução. Lembra: o cosseno de algum ângulo está sempre entre e , nunca além disso!
Podemos olhar para essa relação aqui ó, que encontramos no passo :
Antes de cortar dos dois lados o . Essa relação pode ser satisfeita, tomando o valor pro período, quando , pois daí seria satisfeito:
Pois e daí teríamos uma igualdade. E esse ângulo representa a conta embaixo do aro. Então nesse valor de período a conta não iria subir.