Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.5 - Ex. 46
Um ovo é atirado verticalmente de baixo para cima de um ponto próximo da cornija na extremidade superior de um edifício alto. Ele passa rente da cornija em seu movimento para baixo, atingindo um ponto a abaixo da cornija após deixar a mão do lançador. Despreze a resistência do ar. a) Calcule a velocidade inicial do ovo. b) Qual a altura máxima atingida acima do ponto inicial do lançamento? c) Qual o módulo da velocidade nessa altura máxima? d) Qual o módulo e o sentido da aceleração nessa altura máxima? e) Faça gráficos de , e para o movimento do ovo.
Passo 1
Como a resistência do ar é ignorada, o ovo está em queda livre e tem aceleração constante da gravidade, já conhecida por nós.
Vamos tomar o referencial para baixo como .
Sabemos que quando atinge a altura máxima, o ovo para e volta a cair, no instante que ele para, a sua velocidade é igual a zero.
Passo 2
- Queremos saber a velocidade inicial, e temos os deguintes dados:
- Temos agora, a velocidade inicial, .
- Na altura máxima:
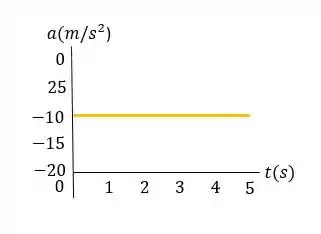
- A aceleração é constante e igual a , para baixo, em todos os pontos do movimento, inclusive na altura máxima.
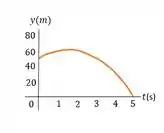
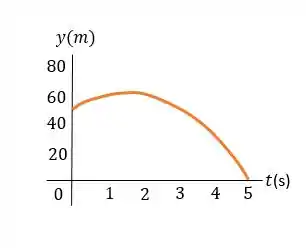
- No primeiro gráfico, temos a posição do ovo nos primeiros .
Vamos usar a equação:
Passo 3
Então, podemos calcular a altura, , máxima, atingida acima do poto inicial do lançamento.
Como aqui, não temos o tempo, e precisamos da posição, , podemos usar a equação de Torricelli:
Passo 4
Passo 5
Passo 6
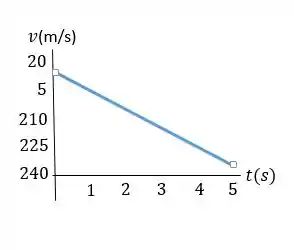
No segundo gráfico, temos que a velocidade é linear.
No tercerceiro gráfico, a sua aceleração constante.
