Num país frio, a temperatura sobre a superfície de um lago caiu a e começa a formar-se uma camada de gelo sobre o lago. A água sob o gelo permanece a : o gelo flutua sobre ela e a camada de espessura crescente em formação serve como isolante térmico, levando ao crescimento gradual de novas camadas de cima para baixo. (a) Exprima a espessura da camada de gelo formada, decorrido um tempo do início do processo de congelamento, como função da condutividade térmica do gelo, da sua densidade e do calor latente de fusão , bem como da diferença de temperatura entre a água e a atmosfera do lago. Sugestão: Considere a agregação de uma camada de espessura à camada já existent, de espessura , e integre em relação a . (b) No exemplo acima, calcule a espessura da camada de gelo após iniciar-se o congelamento, sabendo que , e .
Passo 1
Vamos seguir a sugestão do enunciado, e começar considerando uma pequena camada de espessura , logo abaixo da camada de gelo de espessura :
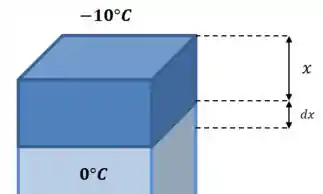
A energia necessária para congelar aquela camada é a seguinte:
Onde é o calor latente de fusão da água. E podemos reescrever aquela massa como:
Então a energia necessária é:
Passo 2
Beleza, agora vamos pensar na taxa com que o calor flui através da camada já congelada:
A camada de gelo tem uma espessura , e está sujeita a uma diferença de temperatura , então:
Onde é a taxa de transmissão de calor por unidade de tempo:
Agora vamos substituir com a fórmula que escrevemos lá em cima:
Vamos reorganizar um pouco:
Agora é só integrar com indo de até um tempo , e a espessura da camada de gelo vai de até um valor .
Passo 3
Integrando os dois lados, temos:
Se no instante inicial não temos nenhum gelo na superfície, então e:
Passo 4
(b) Agora queremos calcular a espessura da camada depois de hora:
E agora é só substituir os valores que foram dados no enunciado na nossa fórmula:
Resposta
(a) A espessura é dada por .
(b) Depois de uma hora a espessura será .