Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 21
Um parquinho está no telhado plano de uma escola, 6,00 m acima da rua (Fig. P3.21). A parede vertical do edifício tem altura de h = 7,00 m, formando uma grade de 1 m de altura ao redor do parquinho. Uma bola caiu na rua abaixo, e um transeunte a devolve jogando a um ângulo de θ = 53,0° acima da horizontal em um ponto d = 24,0 m da base da parede do edifício. A bola leva 2,20 s para alcançar um ponto verticalmente acima da parede. (a) Encontre a velocidade com que a bola foi lançada. (b) Encontre a distância vertical na qual a bola passa acima da parede. (c) Ache a distância horizontal da parede ao ponto no telhado onde a bola cai.
Passo 1
(a)Então, galera, como a bola levou 2,20 segundos até chegar exatamente no ponto acima da grade do parquinho (a do chão), foi esse o tempo que ela levou pra percorrer horizontalmente também a distância . Pela própria figura a gente consegue enxergar melhor isso, beleza?!
Se a gente tem a distância horizontal percorrida e também o tempo do movimento, a gente pode determinar facinho a velocidade horizontal, uma vez que em lançamentos oblíquos ela é constante!
Simplesmente a velocidade horizontal vai valer:
Só que, lembrando de exercícios anteriores, as velocidades horizontal e vertical, na realidade, são decomposições da velocidade original, representada pelo vetorzinho (setinha) na figura saindo do pé do transeunte.
Essas velocidades se correlacionam assim:
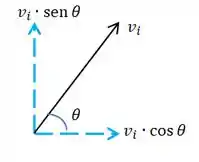
Beleza? E a gente acabou de calcular , a velocidade horizontal, que pelo esqueminha de vetores aí em cima fica representada pela velocidade inicial vezes o cosseno do ângulo com a horizontal.
Nisso, podemos escrever:
E aqui a gente conhece , e . Então a gente determina facilmente a velocidade de lançamento! A gente vai ter:
Passo 2
(b) Vamos denominar a altura que a bola passa exatamente acima da parede da escola por , tudo bem?
A gente sabe o tempo que a bola levou até chegar nesse ponto, dado no enunciado, de 2,20 segundos. Dá pra gente correlacionar com esse tempo pela equação do sorvetão:
Nesse caso, , o deslocamento vertical da bola é justamente a altura que a gente quer determinar; vai ser a velocidade vertical de lançamento da bola, dada por (segundo com o esqueminha do Passo 1), e , a gravidade.
Agora é só aplicar:
Passo 3
(c) O que a gente precisa agora é essa distância daqui, povo, representada pelo tracejado laranja:
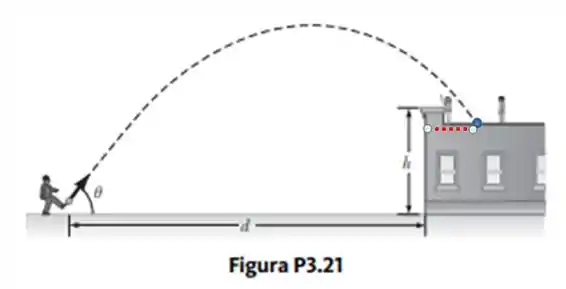
Belê?
Vamos denominar de distância .
Pelo que foi discutido no Passo 1, você vai concordar comigo que pode ser dada pela seguinte expressão:
Onde é a velocidade horizontal da bola, que já conhecemos, e é o tempo decorrido pela bola, desde o lançamento, até o piso do parquinho da escola, tudo bem?
Se a gente determinar , a gente determina e matamos o problema!
E determinar aqui vai ser fácil! Vamos usar sorvetão de novo, nos baseando entre a diferença de altura entre o piso do parquinho e o chão.
Lembra que, aqui, a gente considera o movimento vertical da bola, ok? Vamos aplicar:
Isso vai dar pra gente uma equaçãozinha de segundo grau. Vamos, no próximo passo, deixar ela com uma cara mais amigável e resolver por bhaskara!
Passo 4
A gente vai ter essa equação:
Nisso, temos:
Ok, aqui a gente poderia ter duas respostas, sendo elas:
Só que apenas faz sentido, uma vez que pra bola chegar até antes do parquinho já tinha levado 2,20 segundos, lembra?
Portanto, chegamos a nossa resposta, de
Resposta
(a)
(b)
(c)