Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 92
Uma bola é lançada de um solo plano a um ângulo de 55° acima da horizontal, com uma rapidez inicial de 22 m/s. Ela cai sobre uma superfície dura e repica, atingindo uma altura máxima igual a 75 por cento daquela atingida no primeiro arco de trajetória. (Ignore a resistência do ar.) (a) Qual é a altura máxima atingida no primeiro arco parabólico? (b) A que distância horizontal do ponto de lançamento a bola caiu pela primeira vez? (c) A que distância horizontal do ponto de lançamento a bola caiu pela segunda vez? Suponha que a componente horizontal da velocidade se mantém constante, na colisão da bola com o chão. Dica: Você não pode supor que a bola abandona o chão, após a colisão, a um mesmo ângulo acima da horizontal que no lançamento inicial.
Passo 1
a) Oi pessoal, tudo bem? A gente tem uma bola que quica. Aí ele diz que a altura máxima depois que ela quica é da altura máxima do lançamento inicial:
A figura abaixo vai nos ajudar a entender melhor o enunciado:
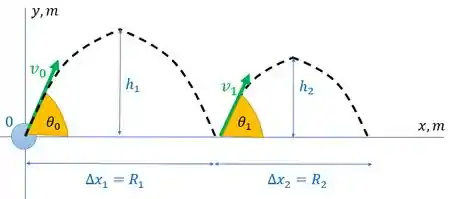
Como ele diz para gente considerar que o ângulo que a bola deixa o chão não é igual nas duas partes do movimento, a gente deixou os dois ângulos como sendo diferentes.
Percebe então que é como se a gente tivesse dois lançamentos de projetil. Um após o outro. Assim, a velocidade na horizontal é constante. E ele fala para considerar ela igual para os dois movimentos, então:
E a aceleração na vertical é constante.
O que ele quer primeiro é a altura máxima . Então a gente só precisa olhar para o primeiro lançamento. Vamos ver como achar essa belezinha!
Passo 2
Se a gente quer a altura máxima, queremos uma informação do movimento vertical, certo? Então a gente só vai olhar para esse movimento.
Para começar, podemos encontrar a velocidade inicial vertical . Ela é a projeção de em . E por isso tem essa expressão:
Outra coisa muito importante é a gente lembrar que no ponto mais alto da sua trajetória, a velocidade vertical do objeto é nula. Então no ponto momento onde ele está no ponto mais alto, temos:
Se temos aceleração constante, valem as equações para o movimento com aceleração contante, certo?
E não temos nada falando sobre tempo decorrido também. Essa é uma dica para gente usar a equação de Torricelli, que relaciona o deslocamento do progétil com a sua velocidade final e inicial. Ela tem essa carinha
Para usar essa bonita para o nosso caso, vamos substituir nossos dados. Lembrando que (negativa porque a gravidade está para baixo. E queremos achar . Substituido essas coisas e nossas expressões:
Isolando quem a gente quer:
Substituindo os valores, temos:
Passo 3
b) Para achar o alcance máximo no primeiro lançamento, vamos achar primeiro o tempo que leva para a bola chegar a altura máxima.
A gente pode usar a equação horária da velocidade para o movimento vertical:
Lembrando que , e na altura máxima temos , e substituindo essas coisas na equação acima:
Esse é o tempo que a bola leva para subir. O tempo total do primeiro lançamento vai ser o dobro disso, então:
Passo 4
Agora que a gente sabe o tempo total do primeiro lançamento, a gente pode descobrir o deslocamento horizontal dentro desse tempo que é o alcance .
Como temos um movimento de velocidade constante na horizontal, a gente pode usar a expressão da velocidade média:
Sendo que e (velocidade inicial horizontal), e temos a expressão de :
Substituindo nossos dados:
Passo 5
c) Ele quer a distância que a bola cai no segundo lançamento em relação ao ponto inicial do primeiro lançamento. Ou seja, a gente quer a soma dos dois alcances dos dois lançamentos:
Já temos , só falta . Os lançamentos são analagos. A bola sai do solo e depois volta. Por isso, a gente pode usar a expressão no alcance que a gente achou para primeiro lançamento:
Mas esse agora é a velocidade inicial do segundo lançamento, que no nosso desenho é . E é o ângulo inicial do lançamento, que agora é . Então fica:
A gente não pode supor que . Então precisamos achar e .
Passo 6
é o módulo da velocidade que tem componentes e . Então o módulo da velocidade é
Substituindo isso na nossa equação do alcance:
A componente inicial da velocidade do segundo lançamento pode ser encontrada usando a equação:
Isso porque por ela a gente acha a altura máxima do segundo lançamento em função da velocidade inicial. Temos que , (velocidade vertical na altura máxima) e:
Isolando , porque queremos ela mesmo:
Como , podemos dizer que:
O enunciado diz que componente horizontal da velocidade no segundo momento é igual a velocidade inicial do primeiro lançamento, então:
Passo 7
Com as componentes da velocidade inicial, a gente pode achar seu ângulo pela formulinha:
Substituindo os valores, temos:
E voltamos ao alcance 2:
Substituindo as expressões de e :
E substitundo os dados:
Portanto: