Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 38
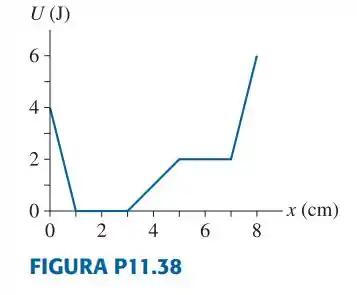
Uma partícula de tem a energia potencial representada na FIGURA P11.38.
a. Desenhe o gráfico força versus posição desde até .
b. Que trabalho realiza a força quando a partícula se move de para ?
c. Qual é o módulo da velocidade que a partícula deve ter em a fim de chegar em com velocidade de ?
Passo 1
Assim como temos , nós podemos associar trabalho e energia potencial da seguinte maneira:
Onde e que ele mede a diferença entre o estado final e o inicial, logo no intervalo entre e nós termos:
Já que temos uma reta e a variação em uma reta é constante.
No intervalo entre temos:
No intervalo entre e a força aplicada será de:
Agora no intervalo entre e
E no intervalo entre e :
Isso nos dá o seguinte gráfico:
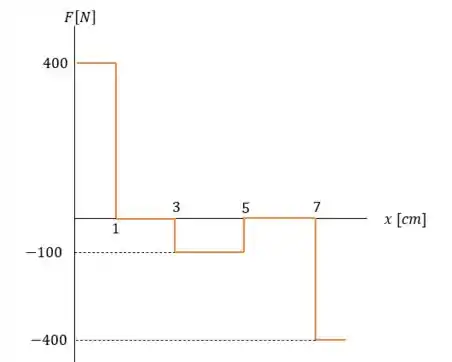
Passo 2
Respondendo a letra , sabendo que a massa da partícula é de nós teremos um trabalho de:
Onde se comporta como no gráfico anterior, ou seja, no intervalo de :
Então:
Passo 3
Como a energia se conserva então para a letra nós vamos ter:
Ou seja a energia mecânica em é igual a energia mecânica em .
E podemos ver pelo gráfico dado pelo enunciado que e , e como queremos que a partícula de massa tenha velocidade de em logo:
Fazendo essa conta encontramos: