Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 53
Uma patinadora de está deslizando sobre o gelo, diretamente para o norte, a . O gelo possui um baixo coeficiente de atrito estático que impede a patinadora de escorregar lateralmente, todavia . Subitamente, um vento começa a soprar do nordeste e exerce uma força de sobre a patinadora.
a. Use trabalho e energia para determinar o valor de velocidade da patinadora após ter deslizado sob este vento.
b. Qual é o valor mínimo de a fim de que a patinadora continue se movendo diretamente para o norte?
Passo 1
Vamos desenhar o que está acontecendo sabendo que se um vento sopra do nordeste para a patinadora então o vento tem direção para sudoeste (direção de com a horizontal).
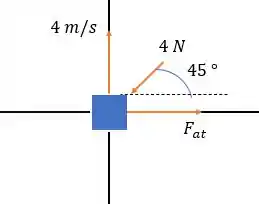
Não ignore a força de atrito que impede a patinadora ir para a horizontal.
Por energia e trabalho temos que:
Onde é o trabalho total de todas as forças atuantes na patinadora. Então:
Porém como a força de atrito está na perpendicular a direção do movimento da patinadora então:
O que nos sobra que pode ser projetada na horizontal e na vertical, porém a projeção na horizontal entra no mesmo caso da e terá trabalho nulo, logo:
Negativo pois ela atrapalha o movimento (é a projeção em da força do vento). Agora como a velocidade final será de:
Passo 2
Agora para a letra temos que fazer a somatória das forças horizontais e que nos dá:
Pois a mínima força de atrito que tem que ter deverá ser igual a força do vento na horizontal, ou seja:
Então o menor valor para é , qualquer valor menor que isso fará a patinadora deslizar para o lado e qualquer valor maior que isso fará a patinadora não se deslocar para o lado.