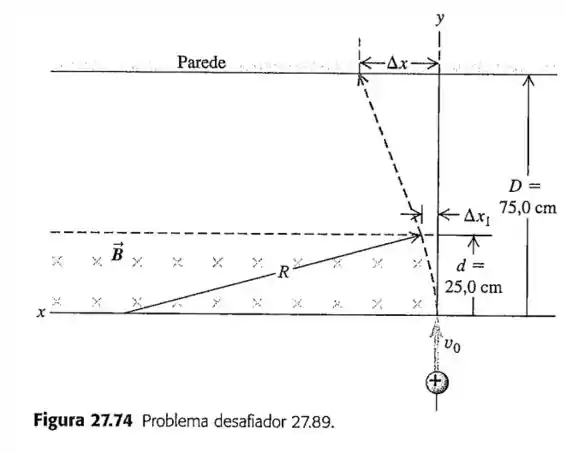
89- Uma partícula com carga igual a 2.15μ C e massa de 3.20 × 10 - 11k g está, inicialmente, se deslocando no sentido + y , com velocidade igual a v 0 = 1.45 × 10 5m / s . Ela, a seguir, entra em uma região onde existe um campo magnético uniforme que entra perpendicularmente no plano da página, como indicado na Figura 27.74 . O módulo do campo é igual a 0.420T . A região se estende até uma distância igual a 25.0c m ao longo da direção inicial do deslocamento; a 75.0c m do ponto onde ela entrou no campo existe uma parede.O comprimento da região onde não existe campo é, portanto, igual a 50.0c m . Quando a partícula carregada entra no campo magnético, ela segue uma trajetória curva com raio de curvatura R . Ela, a seguir, deixa o campo magnético depois de um tempo t 1 , tendo sido desviada de uma distância Δ x 1 . A partícula então se desloca na região sem campo e atinge a parede depois de ser desviada de uma distância total Δ x . a ) Determine o raio R da parte curva da trajetória. b ) Determine t 1 , o tempo durante o qual a partícula permanece no campo magnético. c ) Determine Δ x 1 , o desvio horizontal no ponto onde a partícula sai do campo. d ) Determine Δ x , o desvio horizontal total.

a )R = 5.14m b )t = 1.72 5 × 10 - 6s c ) Δ x 1 = 6.089 × 10 - 3 d )Δ x = 30.46 × 10 - 3 m

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas desafioadores - Ex. 89

89- Uma partícula com carga igual a e massa de está, inicialmente, se deslocando no sentido , com velocidade igual a . Ela, a seguir, entra em uma região onde existe um campo magnético uniforme que entra perpendicularmente no plano da página, como indicado na Figura . O módulo do campo é igual a . A região se estende até uma distância igual a ao longo da direção inicial do deslocamento; a do ponto onde ela entrou no campo existe uma parede.

O comprimento da região onde não existe campo é, portanto, igual a . Quando a partícula carregada entra no campo magnético, ela segue uma trajetória curva com raio de curvatura . Ela, a seguir, deixa o campo magnético depois de um tempo , tendo sido desviada de uma distância . A partícula então se desloca na região sem campo e atinge a parede depois de ser desviada de uma distância total .

Determine o raio da parte curva da trajetória.

Determine , o tempo durante o qual a partícula permanece no campo magnético.

Determine , o desvio horizontal no ponto onde a partícula sai do campo.

Determine , o desvio horizontal total.

Passo 1

O raio da trajetória feita pela partícula é encontrada pela igualdade entre a força magnética e a força centrípeta, ou seja:

Substituindo os valores que o enunciado nos fornece nós teremos:

É surpreendentemente um raio muito longo.

Passo 2

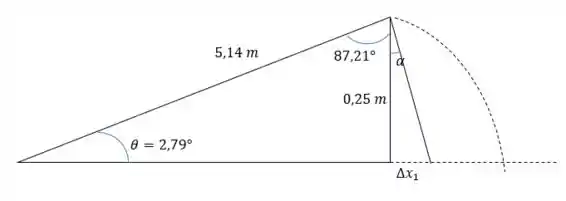
A distância angular percorrida por essa partícula é de:

Onde deve estar em radianos e é vista pelo seguinte triângulo retângulo.

E será:

Então a distância percorrida por essa partícula será:

Como a velocidade dessa partícula é constante em toda a trajetória então:

Passo 3

Vamos desenhar os dois triângulos que temos dentro do campo magnético

Vai ser trabalhoso explicar essa (por que os, mas o ângulo semi-inscrito de pois se traçarmos uma tangente ao círculo formando nós chegamos na seguinte relação

A prova encontra-se aqui.

https://correamani.blogspot.com/2014/08/angulo-de-segmento-ou-angulo-semi.html

De forma que:

Passo 4

A partícula sai com a mesma velocidade com a qual entrou só que ela sai pela tangente. Então temos a seguinte situação.

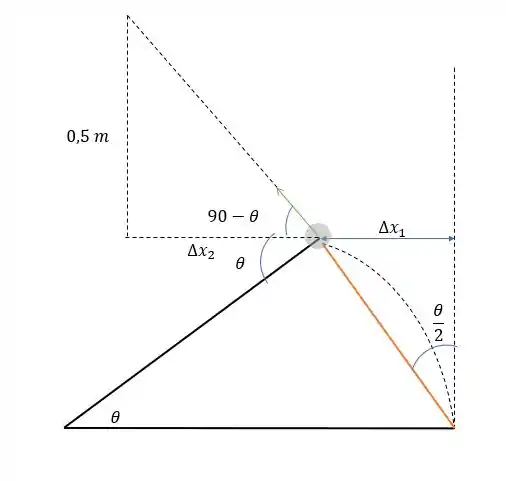
Onde será:

Então será a soma das duas:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reator nuclear. Quando dois núcleos de dêuteron (carga + e , massa 3,34 × 10 - 27 k g ) se aproximam o suficiente, a atração da força nuclear intensa vai fundi-las e produzir um isótopo de hélio, libe

Um dêuteron ( o núcleo de um isótopo do hidrogênio) possui massa igual a 3,34 × 10 - 27 k g e carga + e . O dêuteron descreve uma trajetória circular com raio igual a 6,96 mm em um campo magnético com

Calcule a velocidade de um feixe de elétrons que sofre, simultaneamente, a ação de um campo elétrico de 1,56 × 10 4 V / m e de um campo magnético igual a v x = 4,62 × 10 - 3 T , com ambos os campos or

Um próton ( q = 1,60 × 10 - 19 C ,m = 1,67 × 10 - 27 k g ) se desloca em um campo magnético uniforme B _ = ( 0,500 T )i ^ . Para t=0, o próton possui componentes da velocidade v x = 1,50 × 10 5 m / s

No espectrômetro de massa Bainbridge (Figura 27.24) o módulo do campo magnético no seletor de velocidade é igual a 0,650 T e um íon com velocidade igual a 1,82 × 10 6 m / s não sofre nenhum desvio. (a