Uma partícula está no nível fundamental em uma caixa que se estende desde x = 0 até x = L . a)Qual é a probabilidade de se encontrar a partícula na região entre 0 e L / 4 ? Calcule esse valor integrando Ψ ( x ) 2 d x , onde Ψ é normalizada, desde x = 0 até x = L / 4 . b)Qual é a probabilidade de se encontrar a partícula na região x = L / 4 e x = L / 2 ? c)Como se comparam os resultados dos itens (a) e (b)? Explique. d) Some as probabilidades calculadas nos itens (a) e (b) . e)Os resultados encontrados no itens (a), (b) e (d) estão de acordo com a figura? Explique.

Enunciado

Para uma partícula em uma caixa no estado fundamental :

Como está normalizada:

Para achar a probabilidade, precisamos integrar a norma da função de onda no intervalo dado no enunciado.

letra a)

A probabilidade desde até será:

letra b)

A probabilidade desde até será:

letra c)

Pelos valores das probabilidades que encontramos é mais provável que a partícula esteja mais próxima do meio da caixa do que da borda.

, que é até , é maior que , que é até .

letra d)

Somando:

Os resultados somam exatamente, o que significa que a partícula tem a probabilidade de estar entre e, assim como esteja entre e .

letra e)

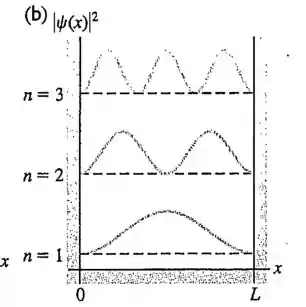
Pela figura temos que é mais provável que a partícula esteja mais próxima do meio da caixa do que da borda.

E esse foi o resultado que encontramos quando calculamos as probabilidades.

Então nosso resultado está de acordo com a figura.

letra a)

letra b)

letra c) é mais provável que a partícula esteja mais próxima do meio da caixa do que da borda.

letra d)

letra e)está de acordo