Exercícios de Partícula no Poço Finito - Lista de Exercícios Resolvida

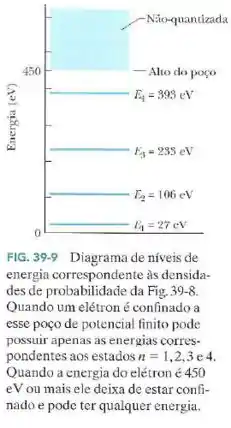
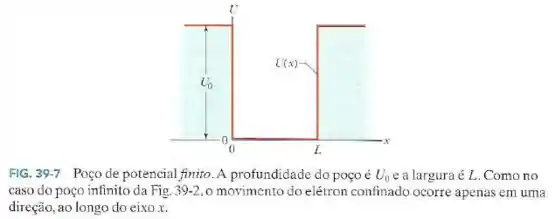
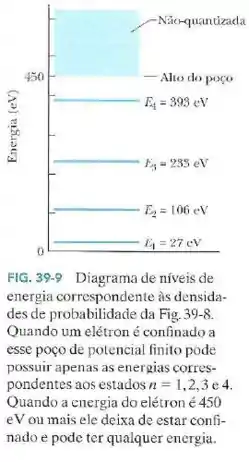
A Fig.39-9 mostra os níveis de energia de um elétron confinado em um poço de potencial finito com de profundidade.

Se o elétron se encontra no estado , qual é a sua energia cinética?

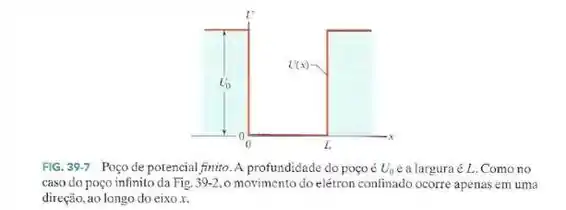
1. Mostre que para região do poço de potencial finito da Fig. 39-7, é uma solução da equação de Schrödinger unidimensional, onde é uma constante e k é um número real positivo.
2. Por que razão a solução matemáticamente aceitável do item (a) não é considerada fisicamente admissível?

Um elétron está confinado no estado fundamental de um

poço finito com

(a) Qual é o maior comprimento de onda de luz capaz de

libertar o elétron do poço de potencial por absorção de um

único fóton?

(b) O elétron, que se encontra inicialmente no estado fun-

damental, pode absorver luz com um comprimento de

onda Se a resposta for afirmativa, qual é a

energia do elétron após a absorção?

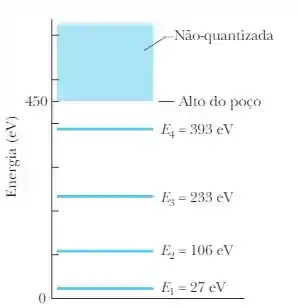
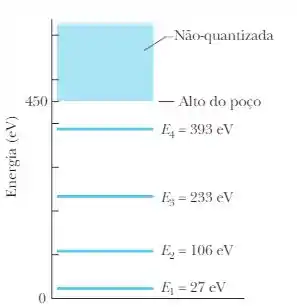
1. Calcule a energia necessária para liberar um elétron no estado fundamental preso num poço finito de potencial , use os valores da figura abaixo.
2. Esboce os gráficos da densidade de probabilidade dos 3 níveis de menor energia no poço.

Um elétron está confinado num poço de potencial finito e a energia necessária para libertá-lo é .

(a) Qual é o maior comprimento de onda de luz capaz de

libertar o elétron do poço de potencial por absorção de um

único fóton?

(b)Qual é a energia do estado em que o elétron se encontra?

(c)Para um comprimento de onda for 4 qual será a energia se o elétron emitir um único fóton?

Um elétron no estado do poço de potencial finito da Fig.39-7 absorve uma energia de de uma fonte externa.

Use o diagrama de níveis de energia da Fig.39-9 para determinar a energia cinética do elétron após essa absorção, supondo que o elétron é transferido para uma posição na qual .

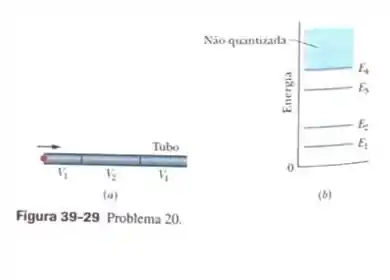
A Fig. 39-29a mostra um tubo fino no qual foi montado um poço de potencial finito, com

Um elétron se move para a direita no interior do poço, em uma região onde a tensão é , com uma energia cinética de . Quando o elétron penetra no poço, pode ficar confinado se perder energia suficiente, emitindo um fóton. Os níveis de energia no interior do poço são e e a região quantizada começa em , como mostra o diagrama de níveis de energia da Fig. 39-29b. Qual é a menor energia (em ) que o fóton pode assumir?

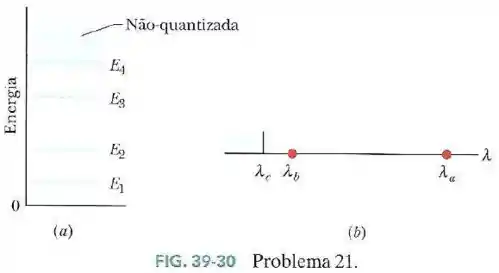
A Fig.39-30a mostra o diagrama de níveis de energia de um poço de potencial unidimensional finito que contém um elétron. A região não quantizada começa em .

A Fig.39-30b mostra o espectro de absorção do elétron quando se encontra no estado fundamental.

O elétron pode absorver fótons com os comprimentos de onda indicados:

, e qualquer comprimento de onda menor que .

Qual é a energia do primeiro estado excitado?

Uma partícula de massa e energia constante , move-se no sentido positivo do eixo na presença de um degrau de potencial.

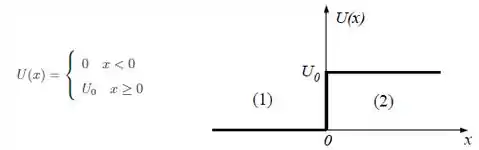
1. Escreva a equação de Schrödinger independente do tempo desta partícula para (região ).
2. Determine a solução geral da equação de Schrödinger na região para . Qual é a solução fisicamente aceitável para o problema? Justifique.
3. Determine a solução geral da equação de Schrödinger na região para . Qual é a solução fisicamente aceitável para o problema? Justifique.

Uma partícula de massa se move em uma dimensão na presença de um “poço de potencial” de profundidade e largura conforme a figura . A partícula se encontra num estado estacionário de energia .

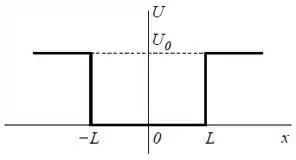
1. A densidade de probabilidade de se encontrar a partícula em uma das regiões fora do poço é , onde e são constantes positivas. Explicite a região fora do poço na qual é aceitável esta densidade e explique o porquê. Calcule a probabilidade de encontrar a partícula nesta região (suponha e conhecidos).
2. Calcule a constante para que a função de onda associada à densidade de probabilidade satisfaça a equação de Schrödinger na região apropriada.
3. Escreva a equação de Schrödinger para a região e determine a solução geral desta equação.

Uma partícula de massa e energia que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.

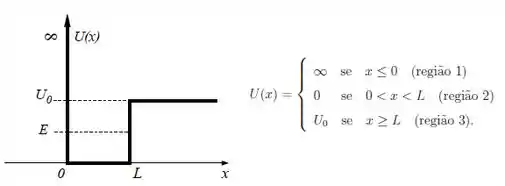
A função de onda estacionária para esta partícula pode ser obtida separadamente em cada região do espaço, sendo assim especificada por:

1. Para o caso , escreva a solução geral para , e , expressando-as, quando for o caso, em termos de combinações lineares das funções e , onde as constantes e são ambas reais e positivas.
2. Calcule os valores de e como função de , e constantes do problema.
3. Que condições de contorno as soluções , e devem satisfazer nos pontos e .

. Uma partícula de massa se move em uma dimensão na presença de um poço de potencial

de profundidade e largura conforme a figura abaixo. A partícula se encontra num estado estacionário de energia .

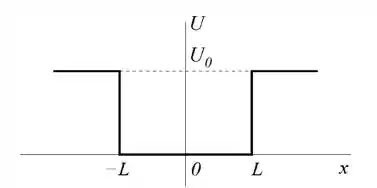
(a) Escreva a equação de Schrödinger independente do tempo desta partícula para e sua solução geral.

(b) Escreva a equação de Schrödinger independente do tempo desta partícula para e e sua solução geral. Qual solução é fisicamente aceitável?

(c) Encontre as condições de contorno que as constantes arbitrárias introduzidas nos itens e devem satisfazer (não é necessário resolver o sistema).

(d) Calcule a probabilidade de encontrar a partícula na região como

função dessas constantes.

Uma partícula de massa m, confinada num poço de potencial como indicado na figura, tem energia total

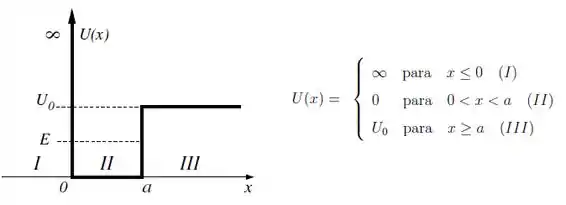
(a) Escreva a solução geral da equação de Schrödinger independente do tempo em termos dos parâmetros do problema. Justificar as respostas através da análise da equação de Schrödinger. Não é necessário encontrar o valor das constantes arbitrárias não nulas.

(b) Escreva as condições de contorno que a função de onda deve satisfazer (não é necessário resolvê-las).

(c) Determine a probabilidade de a partícula estar na região III , em termos das constantes obtidas no item (a).

Uma partícula de massa , confinada num poço de potencial como indicado na figura, tem energia total .

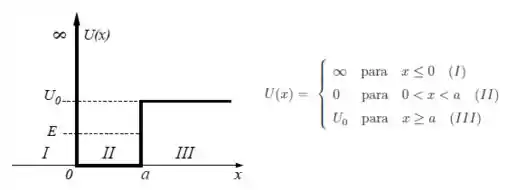
A função de onda da partícula é

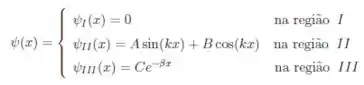
1. Determine a probabilidade da partícula estar na região (), supondo conhecidas as constantes , , , e da função de onda e que ela está normalizada.
2. Determine as constantes e .
3. Escreva as condições de contorno que a função de onda deve satisfazer (não é necessário resolvê-las ).