Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 103

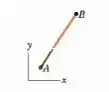
A Fig. 4-53 mostra a trajetória retilínea de uma partícula em um sistema de coordenadas x y quando a partícula é acelerada a partir do repouso em um intervalo de tempo ∆ t 1 . A aceleração é constante. As coordenadas do ponto A são ( 4,00   m ,   6,00   m ) e as do ponto B são ( 12,0   m ,   18,0   m ). (a) Qual é a razão a y / a x , entre as componentes da aceleração? (b) Quais são as coordenadas da partícula se o movimento continua durante outro intervalo igual a ∆ t 1 ?

Passo 1

(a) Primeiro, vamos olhar para o eixo x .

Então pessoal, sabendo que ∆ x = 8,00 m , t =   ∆ t 1   , a = a x e v 0 x = 0 (parte do repouso), temos a fórmula:

∆ x = v 0 x t + a t 2 2

Lembra?? Agora é só substituir as informações e:

8,0   m = a x ∆ t 1 2 2

E a expressão correspondente para o movimento ao longo do eixo y é:

∆ y = 12   m = a y ∆ t 1 2 2

Assim, vamos dividir uma expressão pela outra:

a y ∆ t 1 2 2 a x ∆ t 1 2 2 = 12 8

Podemos fazer as simplificações de ∆ t 1 2 e o 2 que tá dividindo os dois termos. Dessa forma:

a y a x = 12 8 = 1,5

Passo 2

(b) Agora, temos que o movimento ocorreu por mais ∆ t 1 . Então, fazendo t   =   2 ∆ t 1 , nossa equação para tooodo o movimento fica assim:

∆ x = v 0 x t + a t 2 2

Onde v 0 x = 0 , t =   2 ∆ t 1   , a = a x . Dessa forma:

∆ x = a x 2 ∆ t 1 2 2

Mas quem é a x ? Podemos achar ele pela relação do passo anterior, onde tínhamos:

8,0   m = a x ∆ t 1 2 2

Isolando a x :

a x = 16 ∆ t 1 2

Substituindo isso na nossa equação:

∆ x = 16 ∆ t 1 2 2 2 ∆ t 1 2 2

Assim:

∆ x   =   8,0   m 2 2   =   32   m

Isso (32 metros) é o quanto a partícula andou nesse movimento. O que significa que a coordenada x da partícula agora é ( 4,0   +   32 )   m   =   36   m .

Beleza? Vamos fazer a mesma coisa para a coordenada y .

Passo 3

Então, fazendo t   =   2 ∆ t 1 , nossa equação para tooodo o movimento fica assim:

∆ y = v 0 y t + a t 2 2

Onde v 0 y = 0 , t =   2 ∆ t 1   , a = a y . Dessa forma:

∆ y = a y 2 ∆ t 1 2 2

Mas quem é a y ? Podemos achar ele pela relação do passo 1, onde tínhamos:

12 , 0   m = a y ∆ t 1 2 2

Isolando a y :

a y = 24 ∆ t 1 2

Substituindo isso na nossa equação:

∆ y = 24 ∆ t 1 2 2 2 ∆ t 1 2 2

Assim:

∆ y   =   12 , 0   m 2 2   =   48   m

Isso (48 metros) é o quanto a partícula andou nesse movimento. O que significa que a coordenada y da partícula agora é ( 6,0   +   48 )   m   =   54   m .

Tranquilo galera? Bora resolver mais questões então!!!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de um cachorro correndo em um campo aberto possui componentes v x = 2,6m / s , v y = - 1,8m / s para t 1 = 10,0 s . Para o intervalo de tempo entre t 1 = 10,0 s e t 2 = 20,0 s , a acelera
Um avião a jato está voando a uma altura constante. No instante t 1 = 0 , os componentes da velocidade são v x = 90m / s , v y = 110m / s . No instante t 2 = 30,0s , os componentes são v x = - 170 m /
Suponha que a aceleração de uma partícula é uma função de x , onde a x x = 2,0s - 2 x . (a) Se a velocidade é zero quando x = 1,0m , qual é a rapidez quando x = 3,0m ? (b) Quanto tempo a partícula lev
Uma pequena pedra afundando na água experimenta uma aceleração que decai exponencialmente, dada por a y t = g e - b t , onde b é uma constante positiva que depende da forma e tamanhão da pedra e das p
Uma rocha cai através da água com aceleração continuamente decrescente. Assuma que a aceleração da pedra como uma função da velocidade é dada por a y = g - b v y , onde b é uma constante positiva. (A